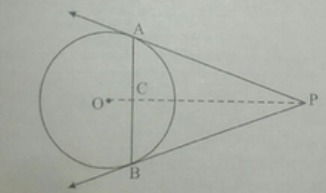
From a point P outside a circle, with centre O, tangents PA and PB are drawn. Prove that
(i) ∠AOP=∠BOP
(ii) OP is the ⊥ bisector of chord AB.
To solve the given problem step by step, we will prove both parts of the question regarding the tangents drawn from point P to the circle.
Given:
- A circle with center O.
- A point P outside the circle.
- Tangents PA and PB drawn from point P to the circle, touching the circle at points A and B respectively.
To Prove:
1. ∠AOP=∠BOP
2. OP is the perpendicular bisector of chord AB.
1. Identify the triangles: Consider triangles AOP and BOP.
2. Identify equal sides:
- Since PA and PB are tangents from point P to the circle, we have:
PA=PB(tangents from a point to a circle are equal)
- The line segment OP is common to both triangles:
OP=OP(common side)
- OA and OB are the radii of the circle:
OA=OB(radii of the same circle)
3. Apply the SAS Congruence Criterion:
- We have two sides and the included angle (OP) equal in both triangles:
△AOP≅△BOP(by SAS)
4. Use CPCTC:
- From the congruence of triangles, we can say:
∠AOP=∠BOP(corresponding parts of congruent triangles)
Part (ii): Prove that OP is the perpendicular bisector of chord AB
1. Join points A and B: Draw line segment AB.
2. Identify the midpoint: Let M be the midpoint of chord AB.
3. Consider triangles OAM and OBM:
- We need to prove that triangles OAM and OBM are congruent.
- OA = OB (radii of the same circle).
- We already established that ∠AOP=∠BOP implies:
∠AOM=∠BOM(since M is the midpoint)
- The segment OM is common to both triangles:
OM=OM(common side)
4. Apply the SAS Congruence Criterion:
- Thus, we have:
△OAM≅△OBM(by SAS)
5. Use CPCTC:
- From the congruence of triangles, we conclude:
AM=MB(corresponding parts of congruent triangles)
6. Show that OP is perpendicular:
- Since ∠OMA=∠OMB and they are equal, we can say:
∠OMA+∠OMB=180∘
- Therefore, ∠OMA=∠OMB=90∘.
7. Conclusion:
- Hence, OP is the perpendicular bisector of chord AB.
Final Conclusion:
We have proved both parts of the question:
1. ∠AOP=∠BOP
2. OP is the perpendicular bisector of chord AB.
- A circle with center O.
- A point P outside the circle.
- Tangents PA and PB drawn from point P to the circle, touching the circle at points A and B respectively.
1. ∠AOP=∠BOP
2. OP is the perpendicular bisector of chord AB.
2. Identify equal sides:
- Since PA and PB are tangents from point P to the circle, we have:
PA=PB(tangents from a point to a circle are equal)
- The line segment OP is common to both triangles:
OP=OP(common side)
- OA and OB are the radii of the circle:
OA=OB(radii of the same circle)
- We have two sides and the included angle (OP) equal in both triangles:
△AOP≅△BOP(by SAS)
- From the congruence of triangles, we can say:
∠AOP=∠BOP(corresponding parts of congruent triangles)
- We need to prove that triangles OAM and OBM are congruent.
- OA = OB (radii of the same circle).
- We already established that ∠AOP=∠BOP implies:
∠AOM=∠BOM(since M is the midpoint)
- The segment OM is common to both triangles:
OM=OM(common side)
- Thus, we have:
△OAM≅△OBM(by SAS)
- From the congruence of triangles, we conclude:
AM=MB(corresponding parts of congruent triangles)
- Since ∠OMA=∠OMB and they are equal, we can say:
∠OMA+∠OMB=180∘
- Therefore, ∠OMA=∠OMB=90∘.
- Hence, OP is the perpendicular bisector of chord AB.
We have proved both parts of the question:
1. ∠AOP=∠BOP
2. OP is the perpendicular bisector of chord AB.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - TANGENTS AND INTERSECTING CHORDSEXERCISE - EXERCISE 18 (B)18videos
TANGENTS AND INTERSECTING CHORDS
- BOOK - ICSECHAPTER - TANGENTS AND INTERSECTING CHORDSEXERCISE - EXERCISE 18 (C)42videos
TANGENTS AND INTERSECTING CHORDS
- BOOK - ICSECHAPTER - TANGENTS AND INTERSECTING CHORDSEXERCISE - EXERCISE 18 (C)42videos
TANGENTS AND INTERSECTING CHORDS
- BOOK - ICSECHAPTER - SPECIMEN QUESTION PAPER (MATHEMATICS)EXERCISE - Section C12videos
SPECIMEN QUESTION PAPER (MATHEMATICS)
- BOOK - ICSECHAPTER - TRIGONOMETRICAL IDENTITIESEXERCISE - QUESTIONS22videos
TRIGONOMETRICAL IDENTITIES
Similar Questions
From a point P outside a circle with centre at C, tangents PA and PB are drawn such that 1(CA)2+1(PA)2=116, then the length of chord AB is
View SolutionIf tangents PA and PB are drawn from P(−1,2) to y2=4x then
View SolutionFrom a point P, two tangents PA and PB are drawn such that PA=10 cm and ∠APB=60∘. Find the length of chord AB.
View SolutionA point P lies outside the circle with centre O. two lines PAOB and PDC are drawn on the circle from P. if PD =OD, then prove that arc BC=3×ArcAD.
View SolutionFrom an external point P, two tangents PA and PB are drawn to the circle with centre O. Prove that OP is the perpendicular bisector of AB.
 View Solution
View SolutionIf from an external point B of a circle with centre O, two tangents BC and BD are drawn such that ∠DBC=120∘, prove that BC+BD=BO.
View SolutionIn the figure, PO⊥QO. The tangents to the circle with centre O at P and Q intersect at a point T. Prove that PQ and OT are right bisectors of each other.
 View Solution
View SolutionTwo tangents TP and TQ are drawn to a circle with centre O from an external point T . Prove that ∠PTQ=2∠OPQ .
View SolutionTwo tangents TP and TQ are drawn to a circle with centre O from an external point T . Prove that ∠PTQ=2∠OPQ .
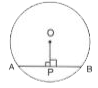
View SolutionThe following figure shows a circle with centre O.
If OP is perpendicular to AB, prove that AP = BP.
 View Solution
View Solution
