In the given PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQ and ∠PAC. If ∠BAQ=30∘, prove that: BD is diameter of the circle.
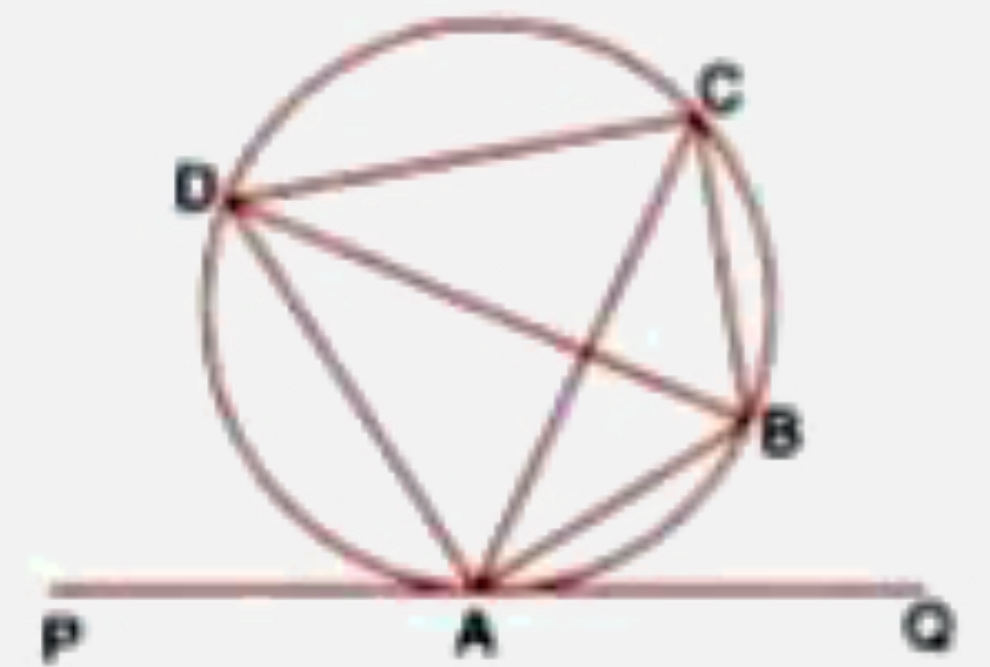
Step by step video & image solution for In the given PQ is a tangent to the circle at A. AB and AD are bisectors of /_CAQ and /_PAC. If /_BAQ=30^(@), prove that: BD is diameter of the circle. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TANGENTS AND INTERSECTING CHORDSBOOK - ICSECHAPTER - TANGENTS AND INTERSECTING CHORDSEXERCISE - EXERCISE 18 (B)
18 Videos
- TANGENTS AND INTERSECTING CHORDSBOOK - ICSECHAPTER - TANGENTS AND INTERSECTING CHORDSEXERCISE - EXERCISE 18 (C)
42 Videos
- TANGENTS AND INTERSECTING CHORDSBOOK - ICSECHAPTER - TANGENTS AND INTERSECTING CHORDSEXERCISE - EXERCISE 18 (C)
42 Videos
- SPECIMEN QUESTION PAPER (MATHEMATICS)BOOK - ICSECHAPTER - SPECIMEN QUESTION PAPER (MATHEMATICS)EXERCISE - Section C
12 Videos
- TRIGONOMETRICAL IDENTITIESBOOK - ICSECHAPTER - TRIGONOMETRICAL IDENTITIESEXERCISE - QUESTIONS
22 Videos
Similar Questions
In the given figure PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQand∠PAC. If ∠BAQ=30∘, prove that :
(i) BD is a diameter of the circle.
(ii) ABC is an isosceles triangle

View SolutionIn the given figure, ∠COB=40∘,AB is the diameter of the circle. Find ∠CAB:

View SolutionIn the given figure, a diameter PQ of a circle bisects the chord RS at the point O. If PS is parallel to RQ, prove that RS is also a diameter of the circle.
View SolutionIn the following figure PQ is the tangent to the circle at A, DB is the diameter and O is the centre of the circle. If ∠ADB=30∘ and ∠CBD=60∘. Calculate :

(i) ∠QAB
(ii) ∠PAD
(iii) ∠CDB
View SolutionProve that the diameter is the greatest chord in a circle.
View SolutionProve that the diameter is the greatest chord in a circle.
View SolutionIf bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.
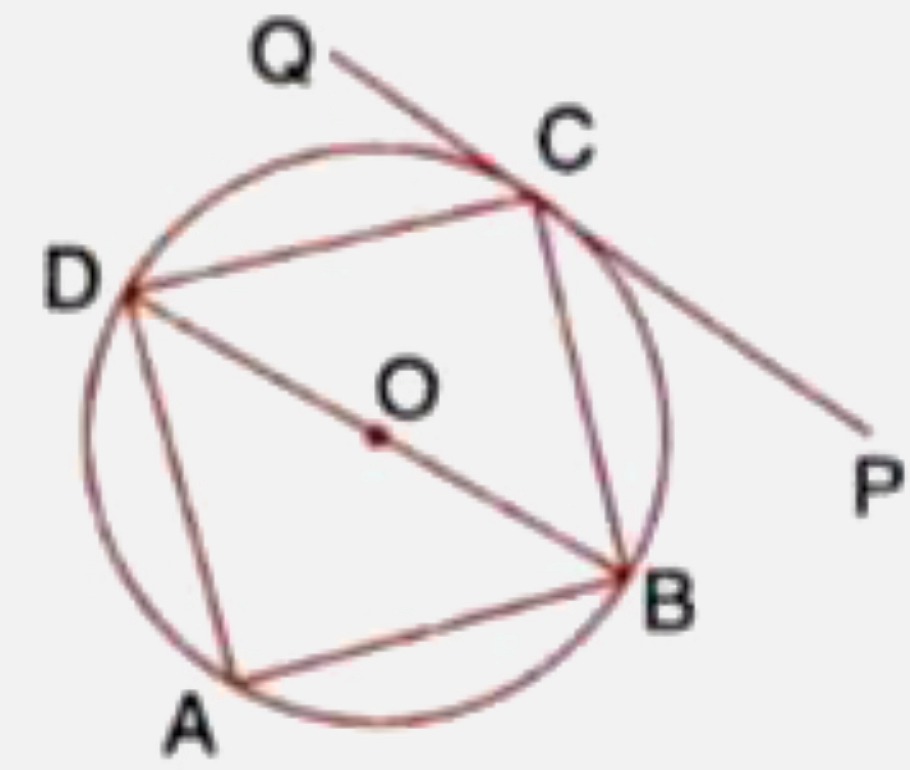
View SolutionIn the given figure, ABCD is a cyclicquadrilateral, PQ is tangent to the circle at point C and BD is its diameter.
If ∠DCQ=40∘ and ∠ABD=60∘ find
(i) ∠DBC
(ii) ∠BCP
(iii) ∠ADB
View SolutionIn the figure, PO⊥QO. The tangents to the circle with centre O at P and Q intersect at a point T. Prove that PQ and OT are right bisectors of each other.

View SolutionIn the adjoining figure, O is the centre of a circle in which AB and CD are two diameters. Prove that AC| |BD and AD| |BC. If ∠OBD=50∘, then find the value of ∠AOC.

View Solution
