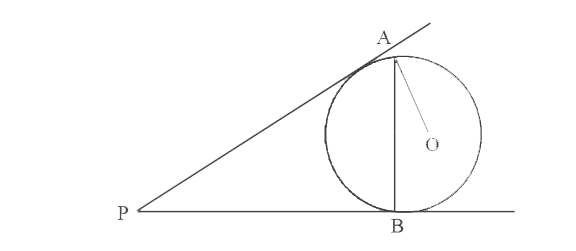
From a point P, two tangents PT and PS are drawn to a circle with centre O such that ∠SPT=120∘ Prove that OP = 2PS.
The correct Answer is:⇒ OP=2PS
Hence, proved
Step by step video, text & image solution for From a point P, two tangents PT and PS are drawn to a circle with centre O such that angleSPT = 120^@ Prove that OP = 2PS. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Similar Questions
Knowledge Check
- Question 1 - Select One
From a point P, two tangents PA and PB are drawn to a circle with centre O. If OP is equal to diameter of the circle, then ∠APBis
A45∘B90∘C30∘D60∘
In Figure, two tangents ABandAC are drawn to a circle with centre O such that ∠BAC=1200. Prove that OA=2AB
View SolutionFrom a point P , two tangents PA and PB are drawn to a circle with centre O . If OP= diameter of the circle, show that APB is equilateral.
View SolutionFrom a point P, two tangents PA and PB are drawn to a circle with centre O and radius r. If OP=2r, show that △APB is equilateral.
 View Solution
View SolutionTwo tangent segments BC and BD are drawn to a circle with centre O and radius r such that ∠DBC=120∘. Prove that BO=2BC.
View SolutionTwo tangents TP and TQ are drawn to a circle with centre O from an external point T . Prove that ∠PTQ=2∠OPQ .
View SolutionFrom an external point P, two tangents PT and PS are drawn to a circle with centre O and radius r. if OP=2r, show that ∠OTS=∠OST=30∘
View SolutionTwo tangents PA and PB are drawn to a circle with centre O from an external point P. Prove that ∠APB=2∠OAB
 View Solution
View Solution

