Given A(0,0) and B(x,y)with xε(0,1) and y>0. Let the slope of the line AB equals m1 Point C lies on the line x=1 such that the slope of BC equals m2 where 0<m2<m1 If the area of the triangle ABC can expressed as (m1−m2)f(x), then largest possible value of f(x) is:Solution in Bengali
1
1/2
1/4
1/8
The correct Answer is:D
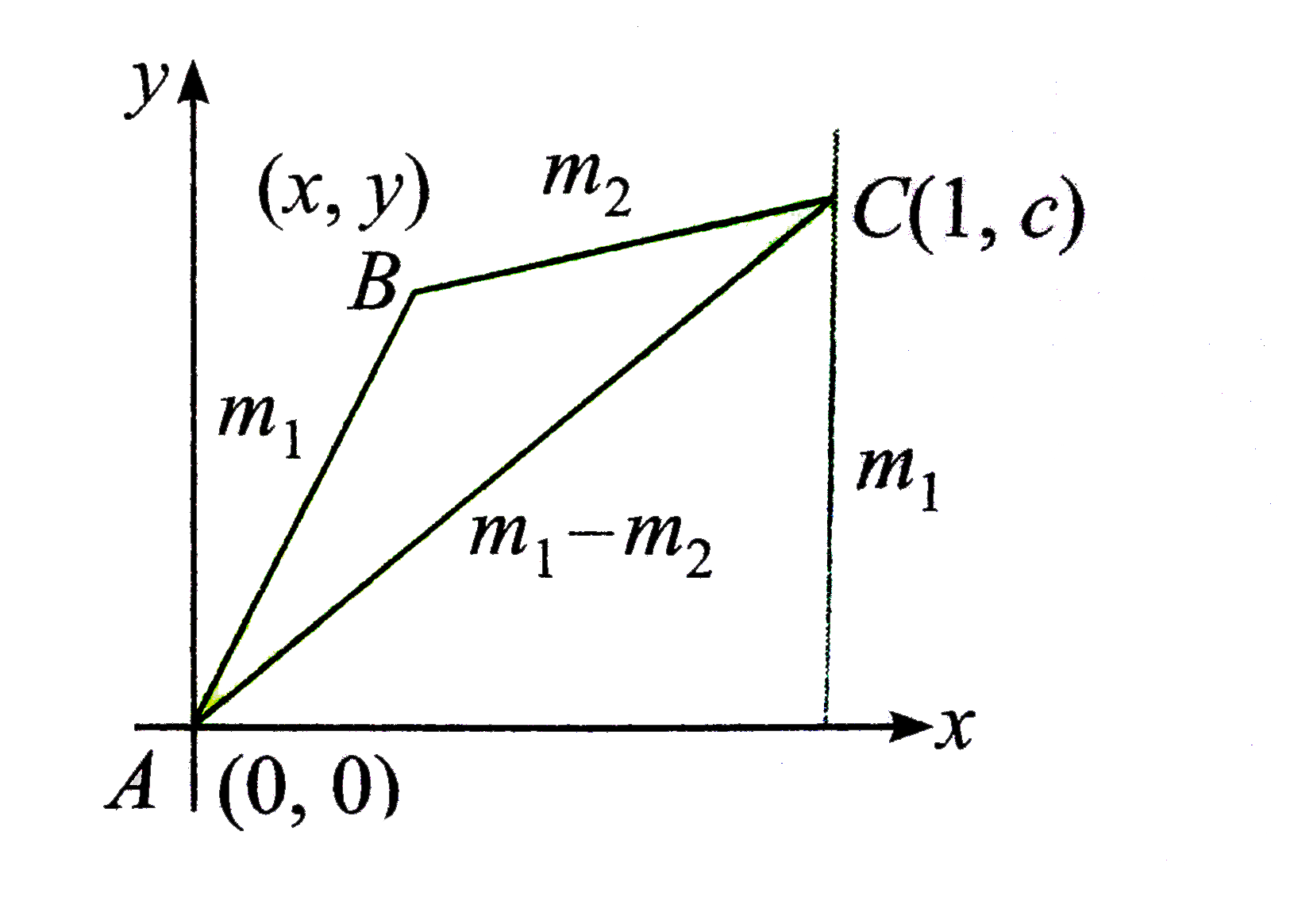
Let the coordinates of C be (1,c). Then,
m2=c−y1−x
or m2=c−m1x1−x
or m2−m2x=c−m1x
or (m1−m2)x=c−m2
or c=(m1−m2)x+m2 (1)
Now, the area of ΔABC is
12∣∣
∣∣∣∣
∣∣001xm1x11c1∣∣
∣∣∣∣
∣∣=12|[cx−m1x]|
=12|[{(m1−m2)x+m2}x−m1x]|
=12∣∣[(m1−m2)x2+m2x−m1x]∣∣
=12(m1−m2)(x−x2) [∵x>x2in(0,1)]
Hence, f(x)=12(x−x2)
f(x)max=18when x=12
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (MULTIPLE CORRECT ANSWERS TYPE)30videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (LINKED COMPREHENSION TYPE)27videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.65videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )1videos
THEORY OF EQUATIONS
Similar Questions
If P is a point (x,y) on the line y=−3x such that P and the point (3, 4) are on the opposite sides of the line 3x−4y=8, then x>815 (b) x>85 y<−85 (d) y<−815
03:52View SolutionLet l be the line belonging to the family of straight lines (a+2b)x+(a−3b)y+a−8b=0,a,b∈R, which is farthest from the point (2,2), then area enclosed by the line L and the coordinate axes is
03:08View SolutionIf aandb are two arbitrary constants, then prove that the straight line (a−2b)x+(a+3b)y+3a+4b=0 will pass through a fixed point. Find that point.
01:50View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
02:43View SolutionGiven A(0,0) and B(x,y) with x∈(0,1) and y>0. Let the slope of line AB be m1. Point C lies on line x=1 such that the slope of BC is equal to m2 where0<m2<m1 If the area of triangle ABC can be expressed as (m1−m2)f(x) then the largest possible value of x is
View SolutionIf y+3=m1(x+2) and y+3=m2(x+2) are two tangents to the parabola y2=8x, then (a)m1+m2=0 (b) m1+m2=−1 (c)m1+m2=1 (d) none of these
05:55View SolutionIf the equations ax2+2hxy+by2=0andy2−(m1+m2)xy+m1m2x2=0 represent the same curve, find m1+m2andm1m2.
04:35View Solutionमाना एक त्रिभुज की भुजाएँ निम्न है
y=m1x+c1
y=m2x+c2
x=0
तब त्रिभुज का क्षेत्रफल ज्ञात कीजिए|07:01View SolutionIf m1andm2 are the slopes of the lines represented by ax2+2hxy+by2=0, then m1+m2=
04:07View SolutionIf m1,m2(m1>m2) are the slopes of the lines which make an angle of 30∘ with the line joining the points (1,2) and (3,4) , then m1m2=
07:14View SolutionGiven A(0,0) and B(x,y) with x∈(0,1) and y>0. Let the slope of line AB be m1. Point C lies on line x=1 such that the slope of BC is equal to m2 where0<m2<m1. If the area of triangle ABC can be expressed as (m1−m2)f(x) then the largest possible value of x is
06:46View SolutionIf y+3=m1(x+2) and y+3=m2(x+2) are two tangents to the parabola y2=8x, then (a)m1+m2=0 (b) m1+m2=−1 (c)m1+m2=1 (d) none of these
06:48View SolutionGiven A(0,0) and B(x,y)with xε(0,1) and y>0. Let the slope of the line AB equals m1 Point C lies on the line x=1 such that the slope of BC equals m2 where 0<m2<m1 If the area of the triangle ABC can expressed as (m1−m2)f(x), then largest possible value of f(x) is:
05:56View SolutionGiven A(0, 0) and B(x, y) with x∈(0,1) and y>0. Let the slope of the line AB equals m1. Point C lies on the line x = 1 such that the slope of BC equals m2 where 0<m2<m1. If the area the triangle ABC can be expressed as (m1−m2)f(x), then find the largest possible value of f(x).
03:11View Solutionਦਿਖਾਉ ਕਿ ਰੇਖਾਵਾਂ y=m1x+c1,y=m2x+c2 ਅਤੇ x=0 ਦੁਆਰਾ ਬਣੀ ਤ੍ਰਿਭੁਜ ਦਾ ਖੇਤਰਫਲ (c1−c2)22|m1−m2| ਹੈ।
09:35View Solution

