Given below are the diameters of circles (in mm) drawn in a design.
Diameter33−3637−4041−4445−4849−52Number of Circles1517212225
Calculate the mean diameter of the circles, variance and standard deviation.
The correct Answer is:¯x=(A+Σf1y1N×h)
To solve the problem, we need to calculate the mean diameter, variance, and standard deviation of the given data. Here’s a step-by-step solution:
Step 1: Create a Table for the Data
We will create a table to organize the data, including the diameter intervals, mid-values, frequencies, and calculations for the mean.
| Diameter (mm) | Frequency (f_i) | Mid-value (x_i) | f_i * x_i |
|----------------|------------------|------------------|-----------|
| 33 - 36 | 15 | 34.5 | 15 * 34.5 = 517.5 |
| 37 - 40 | 17 | 38.5 | 17 * 38.5 = 654.5 |
| 41 - 44 | 21 | 42.5 | 21 * 42.5 = 892.5 |
| 45 - 48 | 22 | 46.5 | 22 * 46.5 = 1023 |
| 49 - 52 | 25 | 50.5 | 25 * 50.5 = 1262.5 |
Step 2: Calculate the Mid-values
The mid-value for each class interval is calculated as:
- For 33 - 36: (33 + 36) / 2 = 34.5
- For 37 - 40: (37 + 40) / 2 = 38.5
- For 41 - 44: (41 + 44) / 2 = 42.5
- For 45 - 48: (45 + 48) / 2 = 46.5
- For 49 - 52: (49 + 52) / 2 = 50.5
Step 3: Calculate the Total Frequency and Total f_i * x_i
Now, we sum the frequencies and the products of frequency and mid-values:
- Total frequency (N) = 15 + 17 + 21 + 22 + 25 = 100
- Total f_i * x_i = 517.5 + 654.5 + 892.5 + 1023 + 1262.5 = 3350
Step 4: Calculate the Mean Diameter
The mean diameter (μ) is calculated using the formula:
Mean=∑(fi⋅xi)N=3350100=33.5
Step 5: Calculate Variance
To calculate the variance, we first need to find fi∗(xi−mean)2:
| Diameter (mm) | Frequency (f_i) | Mid-value (x_i) | f_i * (x_i - μ)^2 |
|----------------|------------------|------------------|--------------------|
| 33 - 36 | 15 | 34.5 | 15 * (34.5 - 43.5)^2 = 15 * 81 = 1215 |
| 37 - 40 | 17 | 38.5 | 17 * (38.5 - 43.5)^2 = 17 * 25 = 425 |
| 41 - 44 | 21 | 42.5 | 21 * (42.5 - 43.5)^2 = 21 * 1 = 21 |
| 45 - 48 | 22 | 46.5 | 22 * (46.5 - 43.5)^2 = 22 * 9 = 198 |
| 49 - 52 | 25 | 50.5 | 25 * (50.5 - 43.5)^2 = 25 * 49 = 1225 |
Now, we sum fi∗(xi−μ)2:
- Total = 1215 + 425 + 21 + 198 + 1225 = 3084
Now we can calculate the variance:
Variance=∑(fi⋅(xi−mean)2)N=3084100=30.84
Step 6: Calculate Standard Deviation
The standard deviation (σ) is the square root of the variance:
Standard Deviation=√Variance=√30.84≈5.55
Final Results
- Mean Diameter: 43.5 mm
- Variance: 30.84
- Standard Deviation: 5.55
We will create a table to organize the data, including the diameter intervals, mid-values, frequencies, and calculations for the mean.
|----------------|------------------|------------------|-----------|
| 33 - 36 | 15 | 34.5 | 15 * 34.5 = 517.5 |
| 37 - 40 | 17 | 38.5 | 17 * 38.5 = 654.5 |
| 41 - 44 | 21 | 42.5 | 21 * 42.5 = 892.5 |
| 45 - 48 | 22 | 46.5 | 22 * 46.5 = 1023 |
| 49 - 52 | 25 | 50.5 | 25 * 50.5 = 1262.5 |
The mid-value for each class interval is calculated as:
- For 33 - 36: (33 + 36) / 2 = 34.5
- For 37 - 40: (37 + 40) / 2 = 38.5
- For 41 - 44: (41 + 44) / 2 = 42.5
- For 45 - 48: (45 + 48) / 2 = 46.5
- For 49 - 52: (49 + 52) / 2 = 50.5
Now, we sum the frequencies and the products of frequency and mid-values:
- Total f_i * x_i = 517.5 + 654.5 + 892.5 + 1023 + 1262.5 = 3350
The mean diameter (μ) is calculated using the formula:
Mean=∑(fi⋅xi)N=3350100=33.5
To calculate the variance, we first need to find fi∗(xi−mean)2:
|----------------|------------------|------------------|--------------------|
| 33 - 36 | 15 | 34.5 | 15 * (34.5 - 43.5)^2 = 15 * 81 = 1215 |
| 37 - 40 | 17 | 38.5 | 17 * (38.5 - 43.5)^2 = 17 * 25 = 425 |
| 41 - 44 | 21 | 42.5 | 21 * (42.5 - 43.5)^2 = 21 * 1 = 21 |
| 45 - 48 | 22 | 46.5 | 22 * (46.5 - 43.5)^2 = 22 * 9 = 198 |
| 49 - 52 | 25 | 50.5 | 25 * (50.5 - 43.5)^2 = 25 * 49 = 1225 |
- Total = 1215 + 425 + 21 + 198 + 1225 = 3084
Variance=∑(fi⋅(xi−mean)2)N=3084100=30.84
The standard deviation (σ) is the square root of the variance:
Standard Deviation=√Variance=√30.84≈5.55
- Mean Diameter: 43.5 mm
- Variance: 30.84
- Standard Deviation: 5.55
Topper's Solved these Questions
- SELF ASSESSMENT PAPER 1BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 1EXERCISE - SECTION B
10 Videos
- SELF ASSESSMENT PAPER 1BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 1EXERCISE - SECTION C
10 Videos
- SAMPLE QUESTION PAPER 5BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER 5EXERCISE - SECTION C
10 Videos
- SELF ASSESSMENT PAPER 2 BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 2 EXERCISE - SECTION C QUESTIONS
8 Videos
Similar Questions
The measurements of the diameters (in mm) of the heads of 107 screws are given below: Diameter (in mm) 33-35 36-38 39-41 42-44 45-47 No. of screws 10 19 23 21 27. calculate mean diameter of head of screw.
View SolutionThe measurements of the diameters (in mm) of the heads of 107 screws are given below: Diameter (in mm), 33-35, 36-38, 39-41, 42-44, 45-47 No. of screws, 10, 19, 23, 21, 27. Find the mean diameter.
View Solution
Knowledge Check
In the figure below , is on ¯¯¯¯¯¯NL and Q is on ¯¯¯¯¯¯PR . The measurements are given in feet . Both NPQM and MQRL are trapezoids. The area , A , of a trapezoid is given by A=12h(b1+b2) , where h is the height and b1 and b2 are the lengths of the 2 parallel sides.
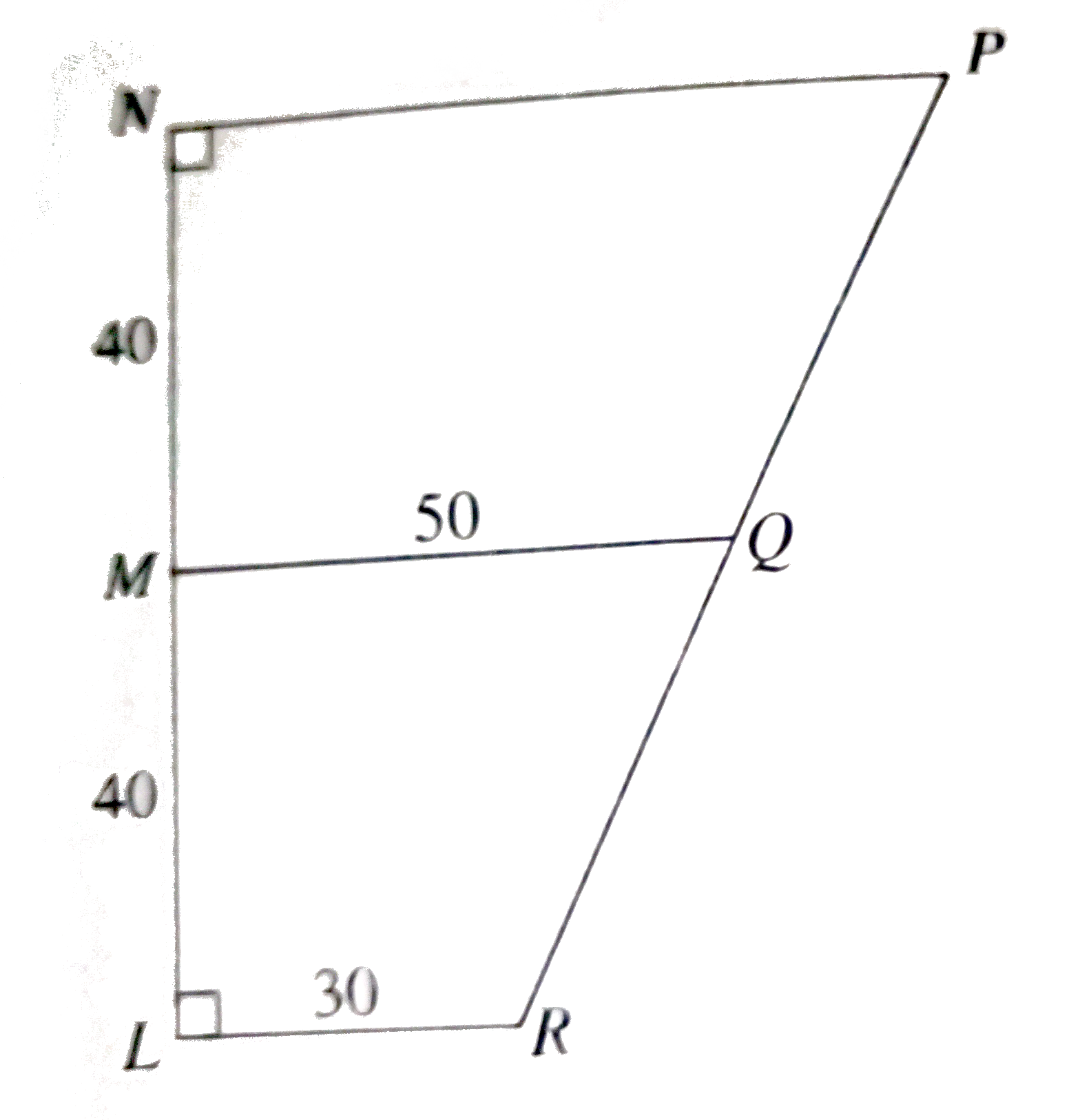
What is the diameter , in feet , of the largest circle that can be drawn inside MNPQ ?A20B40C50D60
The diameter of circles (in mm) drawn in a design are given below:
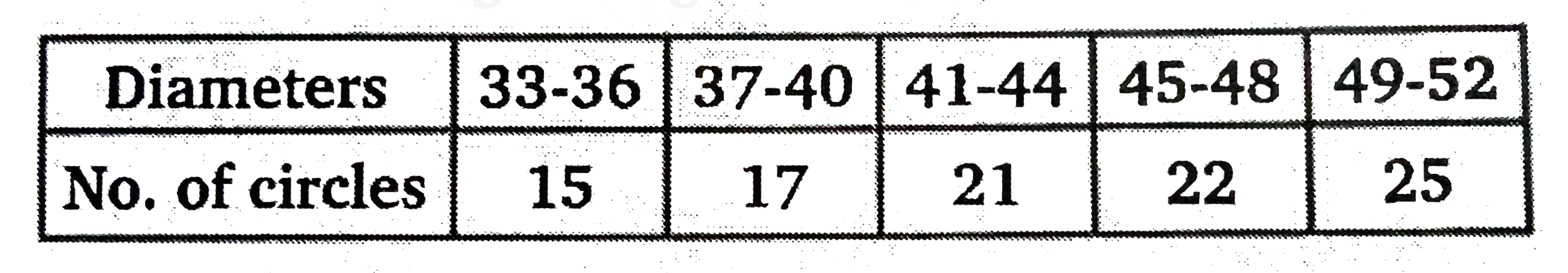
Calculate the standard deviation and mean diameter of the circles.
View SolutionUsing a screw gauge the diameter was measured. The readings are given belwo: 0.39 mm, 0.38 mm, 0.39 mm, 0.41 mm, 0.38 mm, 0.37 m, 0.40 mm,0.39 mm. Calculate (i) the most accurate value of the diameter (ii) the relative error and (iii) percentage error.
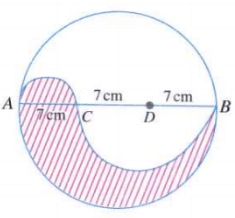
View SolutionGiven is a circle with AB as a diameter of 21 cm. Points C and D lie on the diameter such that AC=7cm,CD=DB=7cm. Semicircles are drawn on the diameter as shown. Find the area of the shaded region.
View SolutionGiven below are the marks obtained by 30 students in an examination :
081733414723203409184214301929113648402422021621153247443301
Taking class intervals 1-10, 11-20 ,......, 41 - 50 , Make a frequency table for the above distribution.
View SolutionFind the area of the following circles, given that:(a) radius = 14 mm (Take ð = 227 ) (b) diameter = 49 m(c) radius = 5 cm
View SolutionFollowing are the marks obtained by 30 students in an examination :
152089101617202430444738364027252830197112131413747232017
Taking class intervals 0-10 , 10-20,............ ., 40-50, construct a frequency table.
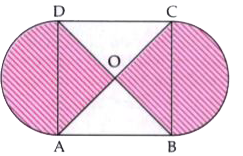
View SolutionIn the given figure, ABCD is a square of side 21 cm. AC and BD are two diagonals of the square. Two semi circles are drawn with AD and BC as diameters. Find the area of the shaded region
(Take π=227)
View Solution
