Using a screw gauge the diameter was measured. The readings are given belwo: 0.39 mm, 0.38 mm, 0.39 mm, 0.41 mm, 0.38 mm, 0.37 m, 0.40 mm,0.39 mm. Calculate (i) the most accurate value of the diameter (ii) the relative error and (iii) percentage error.
To solve the problem step by step, we will follow the instructions provided in the video transcript and calculate the most accurate value of the diameter, the relative error, and the percentage error.
Step 1: Calculate the Most Accurate Value of the Diameter
To find the most accurate value (mean value) of the diameter, we will sum all the readings and divide by the number of readings.
Given readings:
- r1=0.39mm
- r2=0.38mm
- r3=0.39mm
- r4=0.41mm
- r5=0.38mm
- r6=0.40mm
- r7=0.39mm
Calculation:
Sum of readings=r1+r2+r3+r4+r5+r6+r7=0.39+0.38+0.39+0.41+0.38+0.40+0.39=2.74mm
Number of readings=7
Most accurate value(raverage)=Sum of readingsNumber of readings=2.747≈0.3914mm
Step 2: Calculate the Absolute Error for Each Reading
The absolute error for each reading is calculated as:
Δri=raverage−ri
Calculations:
- Δr1=0.3914−0.39=0.0014mm
- Δr2=0.3914−0.38=0.0114mm
- Δr3=0.3914−0.39=0.0014mm
- Δr4=0.3914−0.41=−0.0186mm
- Δr5=0.3914−0.38=0.0114mm
- Δr6=0.3914−0.40=−0.0086mm
- Δr7=0.3914−0.39=0.0014mm
Step 3: Calculate the Average Absolute Error
The average absolute error is calculated as:
Δraverage=∑ΔriNumber of readings
Calculation:
Δraverage=0.0014+0.0114+0.0014−0.0186+0.0114−0.0086+0.00147=0.00047≈0.0000571mm
Step 4: Calculate the Relative Error
The relative error is given by:
Relative Error=Δraverageraverage
Calculation:
Relative Error=0.00005710.3914≈0.000145
Step 5: Calculate the Percentage Error
The percentage error is given by:
Percentage Error=Relative Error×100
Calculation:
Percentage Error=0.000145×100≈0.0145%
Final Answers:
(i) Most accurate value of the diameter: 0.3914mm
(ii) Relative error: 0.000145
(iii) Percentage error: 0.0145%
To find the most accurate value (mean value) of the diameter, we will sum all the readings and divide by the number of readings.
- r1=0.39mm
- r2=0.38mm
- r3=0.39mm
- r4=0.41mm
- r5=0.38mm
- r6=0.40mm
- r7=0.39mm
Sum of readings=r1+r2+r3+r4+r5+r6+r7=0.39+0.38+0.39+0.41+0.38+0.40+0.39=2.74mm
Number of readings=7
Most accurate value(raverage)=Sum of readingsNumber of readings=2.747≈0.3914mm
The absolute error for each reading is calculated as:
Δri=raverage−ri
- Δr1=0.3914−0.39=0.0014mm
- Δr2=0.3914−0.38=0.0114mm
- Δr3=0.3914−0.39=0.0014mm
- Δr4=0.3914−0.41=−0.0186mm
- Δr5=0.3914−0.38=0.0114mm
- Δr6=0.3914−0.40=−0.0086mm
- Δr7=0.3914−0.39=0.0014mm
The average absolute error is calculated as:
Δraverage=∑ΔriNumber of readings
Δraverage=0.0014+0.0114+0.0014−0.0186+0.0114−0.0086+0.00147=0.00047≈0.0000571mm
The relative error is given by:
Relative Error=Δraverageraverage
Relative Error=0.00005710.3914≈0.000145
The percentage error is given by:
Percentage Error=Relative Error×100
Percentage Error=0.000145×100≈0.0145%
(i) Most accurate value of the diameter: 0.3914mm
Topper's Solved these Questions
- BOOK - ICSECHAPTER - UNITSEXERCISE - MODULE 1 (CONCEPTUAL SHORT ANSWER QUESTIONS WITH ANSWERS)5videos
UNITS
- BOOK - ICSECHAPTER - UNITSEXERCISE - MODULE 1 (LONG ANSWER QUESTIONS)3videos
UNITS
- BOOK - ICSECHAPTER - THERMAL RADIATION EXERCISE - SELECTED PROBLEMS (from WIEN.S DISPLACEMENT LAW)14videos
THERMAL RADIATION
- BOOK - ICSECHAPTER - VECTORS SCALARS ELEMENTARY CALCULUS EXERCISE - UNSOLVED PROBLEMS79videos
VECTORS SCALARS ELEMENTARY CALCULUS
Similar Questions
The diameter of a wire as measured by a screw gauge was found to be 0.026 cm, 0.028 cm, 0.029 cm, 0.027cm, 0.024cm and 0.027 cm. Calculate
(i) mean value of diameter
(ii) mean absoulte error
(iii) relative error (iv) percentage error. Also express the result in terms of absolute error and percentage error.View SolutionThe resistivity of the material of a wire of length 1 and diameter d and resistance R is given by ρ=πRd24l. The length of the wire I=100.0 cm is measured using a metre scale with a least count of I mm, the diameter d=0.22 cm is measured using an instrument with a least count of 0.01 cm and resistnce R=5.00 ohm is measured with an accuracy of 0.01 ohm. What is the percentage error? Suggest a method to reduced the percentage error.
View Solution
Knowledge Check
- Question 1 - Select One
The density of a solid ball is to be determined in an experiment. The diameter of the ball is measured with a screw gauge, whose pitch is 0.5mm and there are 50 divisions on the circular scale. The reading on the main scale is 2.5mm and that on circular scale is 20 divisions. if the measured mass of the ball has a relative error of 2%, the relative percentage error in the density is
A0.9%B2.4%C3.1%D4.2%
The measurements of the diameters (in mm) of the heads of 107 screws are given below: Diameter (in mm) 33-35 36-38 39-41 42-44 45-47 No. of screws 10 19 23 21 27. calculate mean diameter of head of screw.
View SolutionThe measurements of the diameters (in mm) of the heads of 107 screws are given below: Diameter (in mm), 33-35, 36-38, 39-41, 42-44, 45-47 No. of screws, 10, 19, 23, 21, 27. Find the mean diameter.
View SolutionIn an experiment to determine the coefficient of viscosity of a liquid using the formual η=πPr48lQ the radius of the capillary tube was measured to be 0.41 mm using an instrument of least count 0.001 cm, length l was measured usinga metre scale as 15 cm. The percentae error in the pressure difference is 0.4% and the percentage error in the volume of the liquid flow out per second Q is 0.3% what is the maximum percentage error in the coefficient of viscosity?
View SolutionA student performs an experiment to determine the Young's modulus of a wire, exactly2m long, by Searle's method. In a partcular reading, the student measures the extension in the length of the wire to be 0.8mm with an uncertainty of ±0.05mm at a load of exactly 1.0kg, the student also measures the diameter of the wire to be 0.4mm with an uncertainty of ±0.01mm. Take g=9.8m/s2 (exact). the Young's modulus obtained from the reading is
View SolutionA student performs an experiment to determine the Young's modulus of a wire, exactly2m long, by Searle's method. In a partcular reading, the student measures the extension in the length of the wire to be 0.8mmwithanuncerta∫yof+- 0.05mmataloadofexactly1.0kg,thestudentalsomeasuresthediameterofthewire→be04mmwithanuncerta∫yof+-0.01mm.Takeg=9.8m//s^(2) (exact). the Young's modulus obtained from the reading is
View SolutionThe diameter of a wire is measured as 0.25 cm using a screw gauge of least count 0.005 cm. The percentage error is
View SolutionThe number of circular divisions of shown screw gauge are 50. It moves 0.5 mm on main scale in one rotation. The diameter of the ball is:
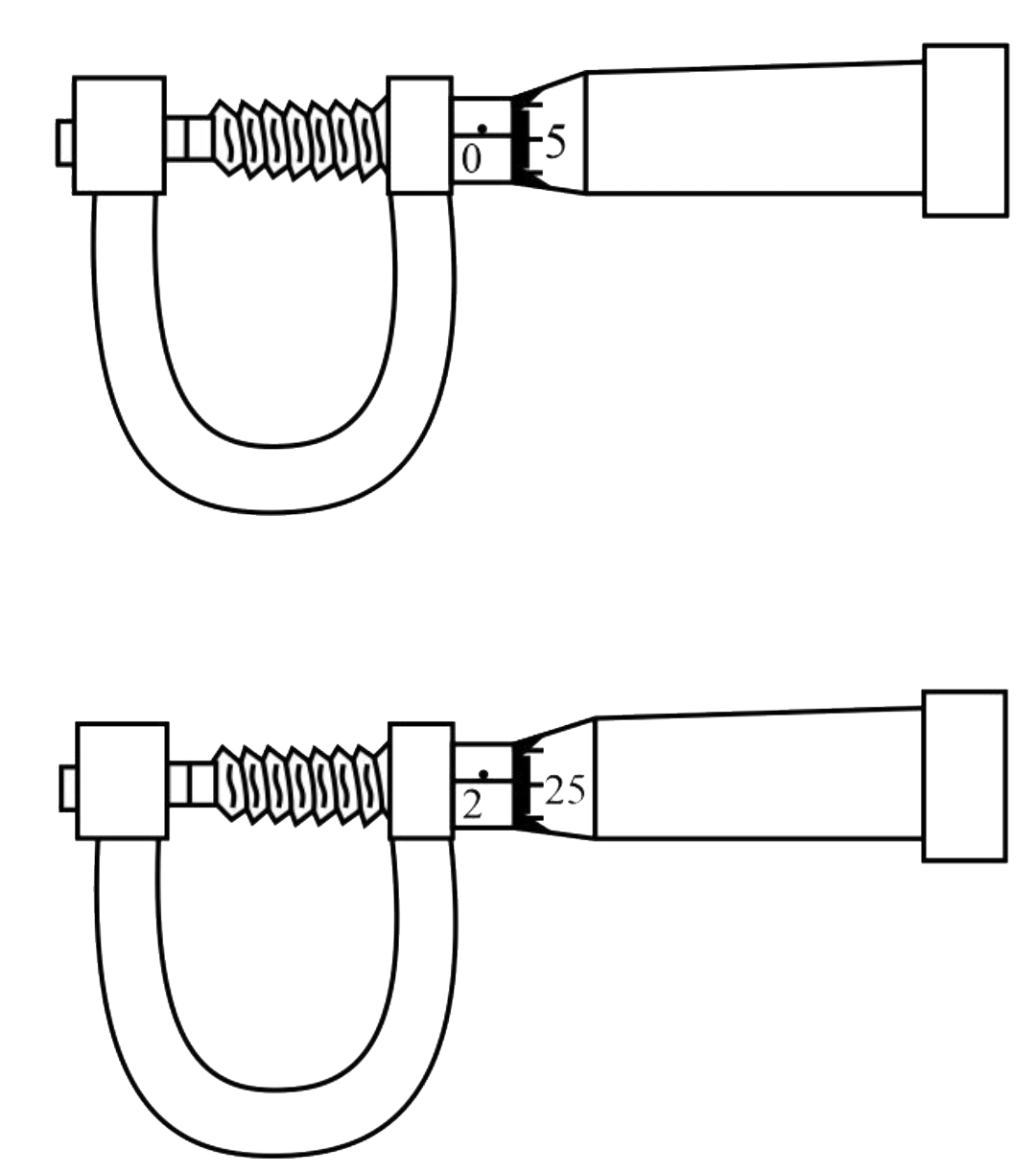 View Solution
View Solution

