The measurements of the diameters (in mm) of the heads of 107 screws are given below: Diameter (in mm), 33-35, 36-38, 39-41, 42-44, 45-47 No. of screws, 10, 19, 23, 21, 27. Find the mean diameter.
To find the mean diameter of the screws based on the given data, we will follow these steps:
Step 1: Create a Continuous Frequency Distribution Table
The given class intervals are not continuous. To make them continuous, we will adjust the class intervals by subtracting 0.5 from the lower limit and adding 0.5 to the upper limit.
Adjusted Class Intervals:
- 33 - 35 becomes 32.5 - 35.5
- 36 - 38 becomes 35.5 - 38.5
- 39 - 41 becomes 38.5 - 41.5
- 42 - 44 becomes 41.5 - 44.5
- 45 - 47 becomes 44.5 - 47.5
Step 2: Calculate the Midpoint (xi) for Each Class Interval
The midpoint (xi) is calculated as the average of the lower and upper limits of each class interval.
- For 32.5 - 35.5: x1=32.5+35.52=34
- For 35.5 - 38.5: x2=35.5+38.52=37
- For 38.5 - 41.5: x3=38.5+41.52=40
- For 41.5 - 44.5: x4=41.5+44.52=43
- For 44.5 - 47.5: x5=44.5+47.52=46
Step 3: Create the Frequency Table
Now we will create a table with the class intervals, their frequencies (fi), and their midpoints (xi).
| Class Interval | Frequency (fi) | Midpoint (xi) | fi * xi |
|----------------|----------------|----------------|---------|
| 32.5 - 35.5 | 10 | 34 | 340 |
| 35.5 - 38.5 | 19 | 37 | 703 |
| 38.5 - 41.5 | 23 | 40 | 920 |
| 41.5 - 44.5 | 21 | 43 | 903 |
| 44.5 - 47.5 | 27 | 46 | 1242 |
Step 4: Calculate the Total Frequencies and Total of fi * xi
Now we need to calculate the total frequency (Σfi) and the total of fi * xi (Σfi * xi).
- Total frequency (Σfi) = 10 + 19 + 23 + 21 + 27 = 100
- Total of fi * xi (Σfi * xi) = 340 + 703 + 920 + 903 + 1242 = 4108
Step 5: Calculate the Mean
The mean (x̄) can be calculated using the formula:
¯x=Σfi⋅xiΣfi
Substituting the values we calculated:
¯x=4108100=41.08
Conclusion
The mean diameter of the screws is 41.08 mm.
---
The given class intervals are not continuous. To make them continuous, we will adjust the class intervals by subtracting 0.5 from the lower limit and adding 0.5 to the upper limit.
- 33 - 35 becomes 32.5 - 35.5
- 36 - 38 becomes 35.5 - 38.5
- 39 - 41 becomes 38.5 - 41.5
- 42 - 44 becomes 41.5 - 44.5
- 45 - 47 becomes 44.5 - 47.5
The midpoint (xi) is calculated as the average of the lower and upper limits of each class interval.
- For 35.5 - 38.5: x2=35.5+38.52=37
- For 38.5 - 41.5: x3=38.5+41.52=40
- For 41.5 - 44.5: x4=41.5+44.52=43
- For 44.5 - 47.5: x5=44.5+47.52=46
Now we will create a table with the class intervals, their frequencies (fi), and their midpoints (xi).
|----------------|----------------|----------------|---------|
| 32.5 - 35.5 | 10 | 34 | 340 |
| 35.5 - 38.5 | 19 | 37 | 703 |
| 38.5 - 41.5 | 23 | 40 | 920 |
| 41.5 - 44.5 | 21 | 43 | 903 |
| 44.5 - 47.5 | 27 | 46 | 1242 |
Now we need to calculate the total frequency (Σfi) and the total of fi * xi (Σfi * xi).
- Total of fi * xi (Σfi * xi) = 340 + 703 + 920 + 903 + 1242 = 4108
The mean (x̄) can be calculated using the formula:
The mean diameter of the screws is 41.08 mm.
Topper's Solved these Questions
Similar Questions
The measurements of the diameters (in mm) of the heads of 107 screws are given below: Diameter (in mm) 33-35 36-38 39-41 42-44 45-47 No. of screws 10 19 23 21 27. calculate mean diameter of head of screw.
View SolutionGiven below are the diameters of circles (in mm) drawn in a design.
Diameter33−3637−4041−4445−4849−52Number of Circles1517212225
Calculate the mean diameter of the circles, variance and standard deviation.
View SolutionThe demand of different shirt sizes, as obtained by a survey, is given below: Size:, 37,38, 39, 40, 41, 42, 43, 44, total No. of Person (wearing it):, 26, 39, 20, 15, 13, 7, 5, 125 Find the modal shirt sizes, as observed from the survey.
View SolutionThe marks obtained by 12 students in an examination (out of 50) are given below:
18, 35, 2, 27, 40, 0, 21, 33, 27, 8, 36, 23
Find the mean marks.
View SolutionThe following table shows the ages of the patients admitted in a hospital during a year: Age (in years): 5-15 15-25 25-35 35-45 45-55 55-65 No. of students: 6 11 21 23 14 5 Find the mode and the mean of the data given above. Compare and interpret the two measures of central tendency.
View SolutionThe marks of 24 candidates in the subject mathematics are given below :
45,48,15,23,30,35,40,11,29,0,3,12,48,18,30,15,30,1,1,42,23,2,3,44
The maximum marks are 50. Make a frequency distribution taking class intervals 0 - 10, 10 - 20, ...............
View SolutionUsing a screw gauge the diameter was measured. The readings are given belwo: 0.39 mm, 0.38 mm, 0.39 mm, 0.41 mm, 0.38 mm, 0.37 m, 0.40 mm,0.39 mm. Calculate (i) the most accurate value of the diameter (ii) the relative error and (iii) percentage error.
View SolutionThe diameter of circles (in mm) drawn in a design are given below:
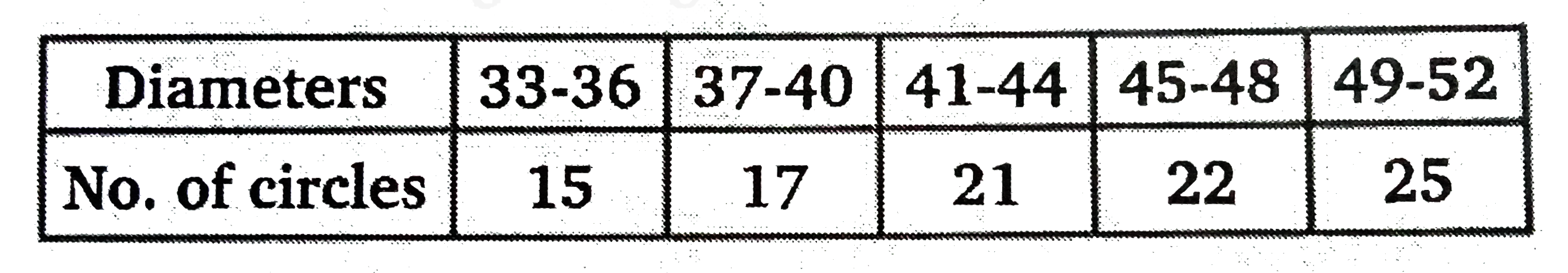
Calculate the standard deviation and mean diameter of the circles.
View SolutionFollowing are the weights (in kg) of 10 new born babies in a hospital on a particular day: 3.4, 3.6, 4.2, 4.5, 3.9, 4.1, 3.8, 4.5, 4.4, 3.6. Find the mean .
View SolutionFollowing are the weights (in kg) of 10 new born babies in a hospital on a particular day: 3.4, 3.6, 4.2, 4.5, 3.9, 4.1, 3.8, 4.5, 4.4, 3.6. Find the mean .
View Solution
