Given P(x)=x4+ax3+bx2+cx+d such that x=0 is the only real root of P'(x)=0. If P(−1)<P(1), then in the interval [−1,1]
P(-1) is the minimum and p(1)the maximum of P
(-1) is not minimum but p(1) the maximum of P
p(-1) is the minimum but P(1) is not the maximum of P
Niether p(-1) is the maxiumum nor P(1) is the maximum of P
The correct Answer is:B
We have
p(x)=x4+ax3+bx2+cx+d
⇒P'(x)=4x3+3ax2+2bx+c
It is gien that x=0 is a root of p'(x)=0
∴P'(0)=0⇒c=0
Putting c=0 , we get
P'(x)=x(4x2+3ax+2b)
Since x=0 is only real root of P'(x)=0. Therefore,
4x2+3ax+2b=0 has no real root
⇒9a2−32b<0
It is given that
P(−1)<P(1)
⇒1−a+b−c+d<1+a+b+c+d
⇒a>0
But , 9a2−32b<0 . Therefore ,b>0
∴P'(x)=x(4x2+3ax+2b)>0 for all x∈(0,1]
⇒ P(x) is increasing in (0,1]
⇒ P(1) is the maximum value of P(x)
Also P'(x)=x(4x2+3ax+2b)<0 for all x∈[−1,0] [∴4x2+3ax+2b>0 for all x]
⇒ P(x) is decreasing in [-1,0]
⇒ P(-1) is not the minimum value of P
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MAXIMA AND MINIMA EXERCISE - Section II - Assertion Reason Type7videos
MAXIMA AND MINIMA
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MAXIMA AND MINIMA EXERCISE - Exercise47videos
MAXIMA AND MINIMA
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MAXIMA AND MINIMA EXERCISE - Chapter Test29videos
MAXIMA AND MINIMA
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MATHEMATICAL REASONING EXERCISE - Chapter Test20videos
MATHEMATICAL REASONING
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MEASURES OF CENTRAL TENDENCYEXERCISE - Chapter Test21videos
MEASURES OF CENTRAL TENDENCY
Similar Questions
Letf(x)=x4+ax3+bx2+cx+d be a polynomial with real coefficients and real roots. If |f(i)|=1where i=√−1, then the value of a +b+c+d is
View SolutionIf the roots of ax3+bx2+cx+d=0 are in G.P then the roots of dx3−cx2+bx−a=0 are in
View SolutionLet P(x)=x2+12x+b and Q(x)=x2+cx+d be two polynomials with real coefficients such that P(x)Q(x)=Q(P(x)) for all real x. Find all the real roots of P(Q(x)) =0.
View SolutionIf P(x)=ax2+bx+c, and Q(x)=−ax2+dx+c,ax≠0 then prove that P(x),Q(x)=0 has atleast two real roots.
View SolutionLet Pn(x)=1+2x+3x2+............+(n+1)xn be a polynomial such that n is even.The number of real roots of Pn(x)=0 is
View SolutionLet a,b,c∈R with a>0 such that the equation ax2+bcx+b3+c3−4abc=0 has non-real roots.
If P(x)=ax2+bx+candQ(x)=ax2+cx+b, then (a) P(x)>0 for all x∈R and Q(x)<0 for all x∈R. (b) P(x)<0 for all x∈RandQ(x)>0 for all x∈R. (c) neither P(x)>0 for all x∈R nor Q(x)>0 for all x∈R. (d) exactly one of P(x) or Q(x) is positive for all real x.View SolutionLet Pn(ix)=1+2x+3x2+............+(n+1)xn be a polynomial such that n is even.The number of real roots of Pn(x)=0 is
View SolutionLet Pn(ix)=1+2x+3x2+............+(n+1)xn be a polynomial such that n is even.The number of real roots of Pn(x)=0 is
View SolutionIn the given figure graph of y=p(x)=x4+ax3+bx2+cx+d is given
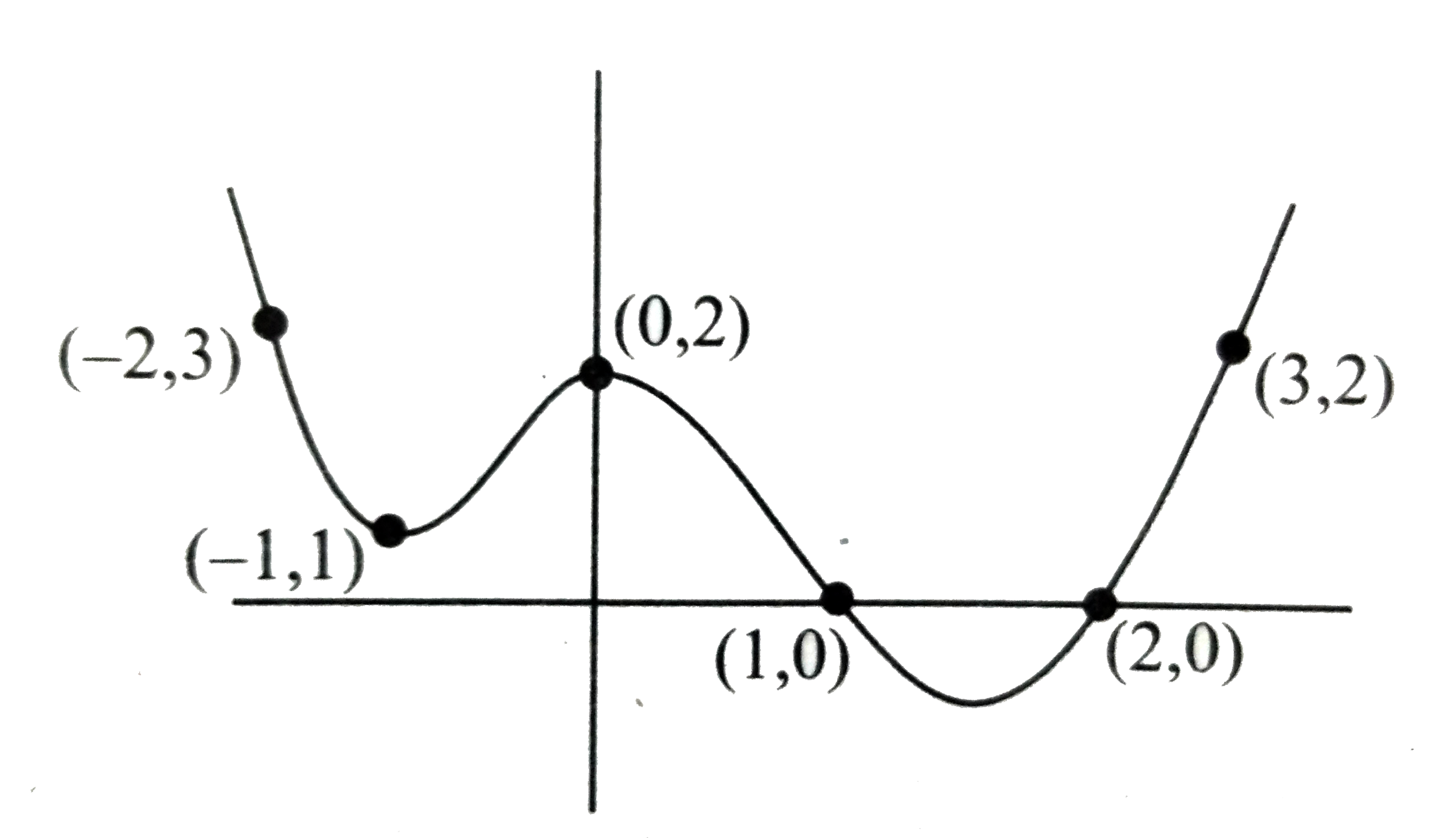
The product of all imaginary roots of p(x)=0 is (a) 1 (b) 2 (c) 13 (d) 14View SolutionLet f(x)=x3+x+1 and P(x) be a cubic polynomial such that P(0) = -1 and roots of f(0) = 1 ; P(x) = 0 are the squares of the roots of f(x) = 0 . Then find the value of P(4).
View Solution

