Given that ABCD is a parallelogram whose diagonals intersect at point. O.∠ABC=110∘,∠ACB=35∘and∠ADB=55∘. The term that best describes ABCD is:
Rectangle
Rhombus
Square
Kite
The correct Answer is:B
To determine the term that best describes the parallelogram ABCD, we will analyze the given angles and properties step by step.
Step 1: Understand the properties of a parallelogram
A parallelogram has opposite sides that are equal and parallel. The diagonals of a parallelogram bisect each other.
Step 2: Identify the given angles
We have the following angles:
- Angle ABC = 110°
- Angle ACB = 35°
- Angle ADB = 55°
Step 3: Use the properties of angles in a parallelogram
Since ABCD is a parallelogram, we know that:
- Angle ABC + Angle ADC = 180° (consecutive angles)
- Angle ACB + Angle BDC = 180° (consecutive angles)
Step 4: Find angle BDC
We can find angle BDC using the fact that angle ADB is equal to angle BDC (alternate interior angles):
- Angle BDC = Angle ADB = 55°
Step 5: Find angle ADC
Now, we can find angle ADC:
- Angle ADC = 180° - Angle ABC = 180° - 110° = 70°
Step 6: Check the properties of the diagonals
Since the diagonals of a parallelogram bisect each other, we can analyze triangle BOC:
- In triangle BOC, we have:
- Angle ACB = 35°
- Angle BDC = 55°
Using the angle sum property:
- Angle BOC = 180° - (Angle ACB + Angle BDC) = 180° - (35° + 55°) = 180° - 90° = 90°
Step 7: Analyze triangle ABC
Now, let's analyze triangle ABC:
- We already know:
- Angle ABC = 110°
- Angle ACB = 35°
To find angle BAC:
- Angle BAC = 180° - (Angle ABC + Angle ACB) = 180° - (110° + 35°) = 180° - 145° = 35°
Step 8: Check for equal sides
Since angle ACB = angle BAC = 35°, we can conclude that sides AB and BC are equal (by the Isosceles Triangle Theorem).
Step 9: Conclusion
In parallelogram ABCD:
- The adjacent sides are equal (AB = BC).
- The diagonals are perpendicular (BD ⊥ AC).
These properties indicate that ABCD is not just a parallelogram, but specifically a rhombus.
Final Answer
The term that best describes ABCD is rhombus.
---
A parallelogram has opposite sides that are equal and parallel. The diagonals of a parallelogram bisect each other.
We have the following angles:
- Angle ABC = 110°
- Angle ACB = 35°
- Angle ADB = 55°
Since ABCD is a parallelogram, we know that:
- Angle ABC + Angle ADC = 180° (consecutive angles)
- Angle ACB + Angle BDC = 180° (consecutive angles)
We can find angle BDC using the fact that angle ADB is equal to angle BDC (alternate interior angles):
- Angle BDC = Angle ADB = 55°
Now, we can find angle ADC:
- Angle ADC = 180° - Angle ABC = 180° - 110° = 70°
Since the diagonals of a parallelogram bisect each other, we can analyze triangle BOC:
- In triangle BOC, we have:
- Angle ACB = 35°
- Angle BDC = 55°
Using the angle sum property:
- Angle BOC = 180° - (Angle ACB + Angle BDC) = 180° - (35° + 55°) = 180° - 90° = 90°
Now, let's analyze triangle ABC:
- We already know:
- Angle ABC = 110°
- Angle ACB = 35°
To find angle BAC:
- Angle BAC = 180° - (Angle ABC + Angle ACB) = 180° - (110° + 35°) = 180° - 145° = 35°
Since angle ACB = angle BAC = 35°, we can conclude that sides AB and BC are equal (by the Isosceles Triangle Theorem).
In parallelogram ABCD:
- The adjacent sides are equal (AB = BC).
- The diagonals are perpendicular (BD ⊥ AC).
The term that best describes ABCD is rhombus.
Topper's Solved these Questions
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - POLYGONS AND QUADRILATERALSEXERCISE - Self Assessment Sheet10videos
POLYGONS AND QUADRILATERALS
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - POLYGONS AND QUADRILATERALSEXERCISE - Self Assessment Sheet10videos
POLYGONS AND QUADRILATERALS
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - PERIMETER AND AREA EXERCISE - SELF ASSESSMENT SHEET10videos
PERIMETER AND AREA
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - POWERS AND ROOTS EXERCISE - UNIT TEST-120videos
POWERS AND ROOTS
Similar Questions
Knowledge Check
- Question 1 - Select One
ABCD is a cyclic quadrilateral whose diagonals intersect at P. If AB=BC,∠DBC=70∘and∠BAC=30∘, then the measure of ∠PCD is:
Aa) 50∘Bb) 35∘Cc) 55∘Dd) 30∘ - Question 2 - Select One
ABCD is a cyclic quadrilateral whose diagonals intersect at E. If ∠BEA = 80∘, ∠DBC = 60∘ and ∠BCD = 40∘, which of the following statements is true?
ABD bisects ∠ADCBAB=BCCDA=DCDAC bisects ∠BCD - Question 3 - Select One
Let ABCD be a parallelogram whose diagonals intersect at P and O be the origin, then OA+OB+OC+OD equals
AOPB2OPC3OPD4OP
In the adjoining figure, ABCD is a rectangle whose diagonals AC and BD intersect at O. If ∠OAB=28∘, find ∠OBC.
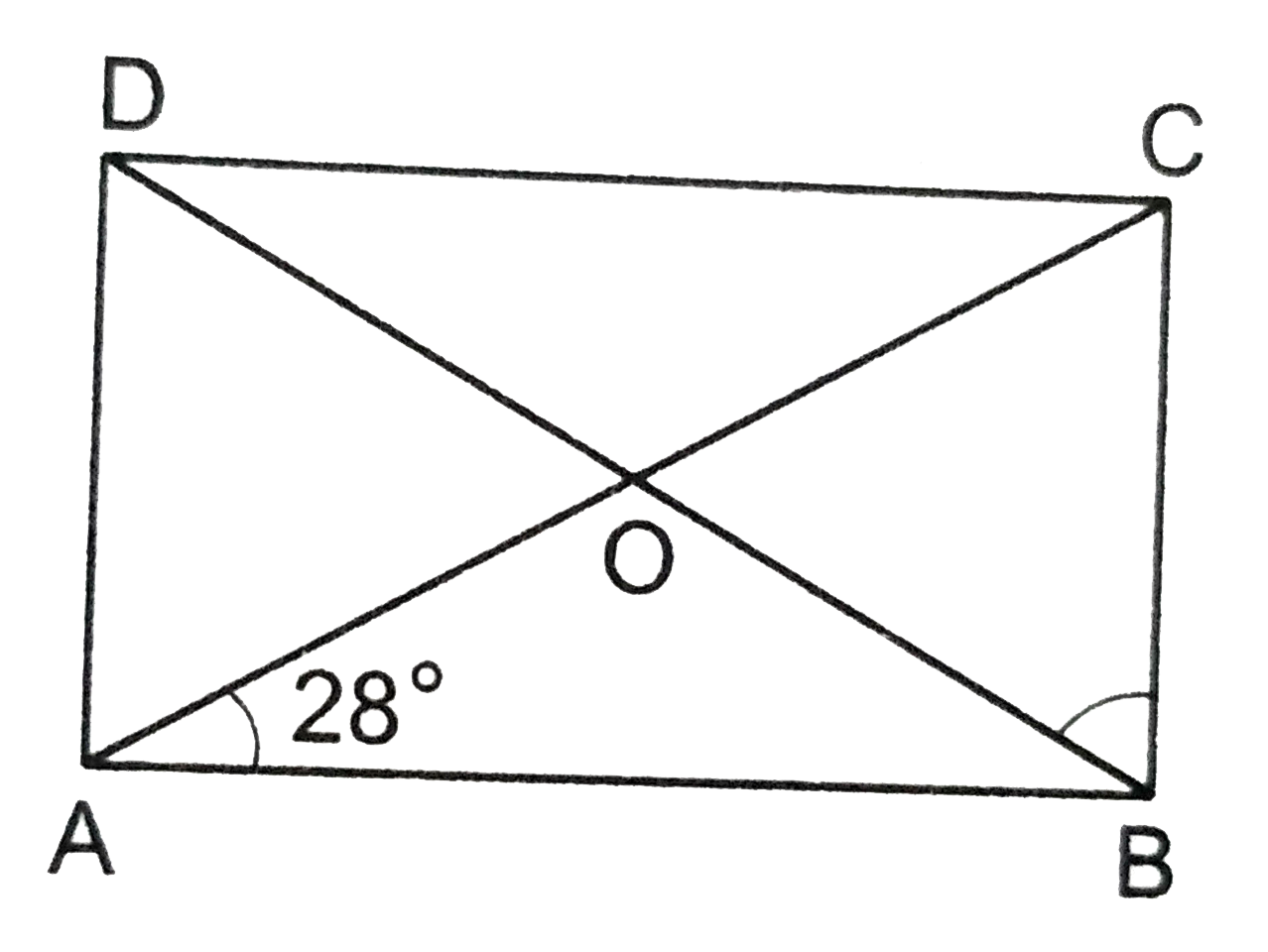 View Solution
View SolutionABCD is a parallelogram in which ∠A=110∘.Find the measure of each of the angles ∠B,∠C and ∠D.
View SolutionABCD is a cyclic parallelogram. The angle ∠B is equal to :
View SolutionIn the given figure, ABCD is a parallelogram, AD = AE, BAE is a straight line, ∠ABC=88∘,∠EAF=162∘and∠AFC=48∘. Then ∠ BCF equals.
 View Solution
View SolutionThe diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC=32∘and∠AOB=70∘, find ∠DBC.
View Solution


