Given that the arithmetic mean and standard deviation of a sample of 15 observations are 24 and 0 respectively. Then which one of the following is the arithmetic mean of the smallest five observation in the data?
0
8
16
24
The correct Answer is:D
To solve the problem, we need to analyze the information given about the sample of 15 observations.
1. Understanding the Given Data:
- We have a sample of 15 observations.
- The arithmetic mean (average) of these observations is 24.
- The standard deviation is 0.
2. Implication of Standard Deviation:
- A standard deviation of 0 indicates that all observations in the sample are identical. This means every observation in the sample is equal to the mean, which is 24.
3. Identifying the Observations:
- Since all observations are the same and equal to the mean, we can conclude that:
- Observation 1 = 24
- Observation 2 = 24
- Observation 3 = 24
- Observation 4 = 24
- Observation 5 = 24
- Observation 6 = 24
- Observation 7 = 24
- Observation 8 = 24
- Observation 9 = 24
- Observation 10 = 24
- Observation 11 = 24
- Observation 12 = 24
- Observation 13 = 24
- Observation 14 = 24
- Observation 15 = 24
4. Calculating the Arithmetic Mean of the Smallest Five Observations:
- The smallest five observations are simply the first five observations since they are all identical and equal to 24.
- Therefore, the smallest five observations are: 24, 24, 24, 24, 24.
5. Finding the Mean of These Observations:
- To find the arithmetic mean of these five observations:
Mean=Sum of observationsNumber of observations=24+24+24+24+245=1205=24
Conclusion:
The arithmetic mean of the smallest five observations in the data is 24.
---
- We have a sample of 15 observations.
- The arithmetic mean (average) of these observations is 24.
- The standard deviation is 0.
- A standard deviation of 0 indicates that all observations in the sample are identical. This means every observation in the sample is equal to the mean, which is 24.
- Since all observations are the same and equal to the mean, we can conclude that:
- Observation 1 = 24
- Observation 2 = 24
- Observation 3 = 24
- Observation 4 = 24
- Observation 5 = 24
- Observation 6 = 24
- Observation 7 = 24
- Observation 8 = 24
- Observation 9 = 24
- Observation 10 = 24
- Observation 11 = 24
- Observation 12 = 24
- Observation 13 = 24
- Observation 14 = 24
- Observation 15 = 24
- The smallest five observations are simply the first five observations since they are all identical and equal to 24.
- Therefore, the smallest five observations are: 24, 24, 24, 24, 24.
- To find the arithmetic mean of these five observations:
Mean=Sum of observationsNumber of observations=24+24+24+24+245=1205=24
The arithmetic mean of the smallest five observations in the data is 24.
Topper's Solved these Questions
- BOOK - NDA PREVIOUS YEARSCHAPTER - SETS, RELATIONS, FUNCTIONS AND NUMBER SYSTEM EXERCISE - MCQ271videos
SETS, RELATIONS, FUNCTIONS AND NUMBER SYSTEM
- BOOK - NDA PREVIOUS YEARSCHAPTER - TRIGONOMETRY - RATIO & IDENTITY , TRIGONOMETRIC EQUATIONSEXERCISE - MCQ238videos
TRIGONOMETRY - RATIO & IDENTITY , TRIGONOMETRIC EQUATIONS
Similar Questions
The mean and the standard deviation (s.d.) of five observations are 9 and 0, respectively. If one of the observations is changed such that the mean of the new set of five observations becomes 10, then their s.d. is
0
1
2
4View SolutionArithmetic mean = (sum of all observations)/(Number of observations)
View Solution
Knowledge Check
- Question 1 - Select One
Given that the arithmetic mean and standard deviation of a sample of 15 observations are 24 and 0 respectively. Then which one of the following is the arithmetic mean of the smallesa five observations in the data?
A0B8C16D24 - Question 2 - Select One
The mean and standard deviations (s.d.) of five observations are 9 and 0 respectively. If one observations is changed such that mean of the new set of five observations becomes 10, then their s.d. is
A0B1C2D4 - Question 3 - Select One
The mean and standard deviation of 6 observation are 8 and 4 respectively. If each observation is multiplied by 3, find the new standard deviation of the resulting observations
A12B18C24D144
The mean and standard deviation of six observations are 8 and 4, respectively. If each observation is multiplied by 3, find the new mean and new standard deviation of the resulting observations.
View SolutionThe mean and standard deviation of 6 observations are 8 and 4 respectively . If each observation is multiplied by 2, find the new mean and new standard deviation of the resulting observation.
View SolutionCalculate mean and standard deviation from the following data:
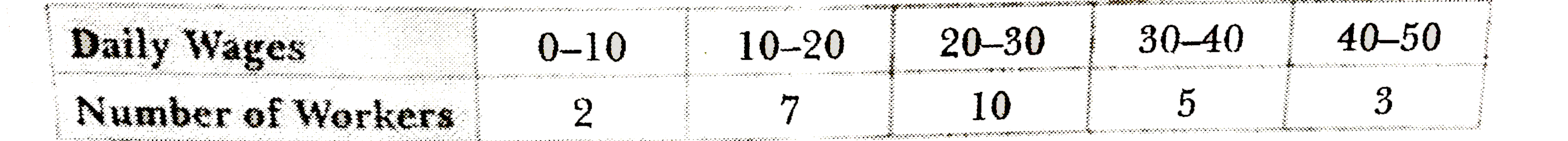 View Solution
View SolutionFind the mean deviation using arithmetic mean from the folloiwng observations:
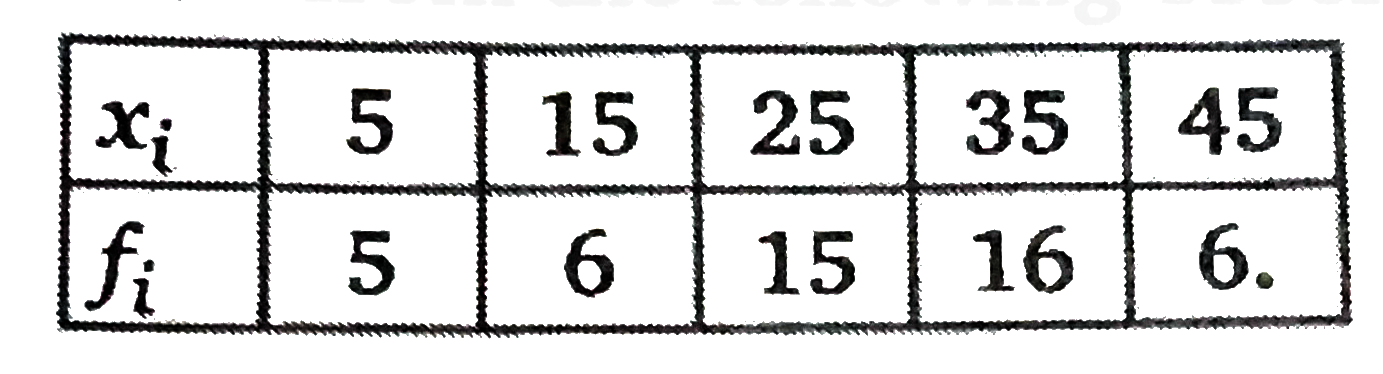 View Solution
View SolutionThe geometric mean and harmonic mean of two non negative observations are 10 and 8 respectively. Then what is the arithmetic mean of the observations equal to?
View Solution

