I is the centre of the incircle of ΔABC, produced AI intersects the circumercile of that triangle at the point P. Prove that PB=PC=PI Solution in Bengali
The correct Answer is:page 279
I is the incentre of ΔABC.
∴∠IBC=∠IBC,∠IAB=∠IACand∠ICB=∠ICA
∴∠IAB=∠IAC.,∴∠PAB=∠PAC
∴B=PC [ by the converse thorem of theore-35 ......(i)
Again, ∠BCPand∠BAP are two angles in circle produced by the are ⌢PB.
∴ by theorem, 35 ∠BCP=∠BAP
or, ∠PBC=∠BAP[∴PB=PC,∴∠BCP=PBC]
Now, external ∠BIPofΔAIB = internally opposite
(∠IAB+∠IBA)=∠IAB+∠IBC
=∠BAP+∠IBC[∴∠IABand∠BAP are same angles]
=∠PBC+∠IBC]
[∴∠PBC=∠BAP]=∠IBP
∴∠BIP+∠IBP
∴ from (1) and (2) we get , PB=PC=PI

Topper's Solved these Questions
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (True or False)
4 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (Short-Answer Type Questions) MCQs
5 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (Short Answer Type Questions)
5 Videos
- THEOREMS RELATED TO CYCLIC QUADRILATERAL BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - Long -answer type questions (L.A.)
12 Videos
- THEOREMS RELATED TO TANGENT IN A CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.2
23 Videos
Similar Questions
In the adjoining figure AD and BE are perpendicular ot BC and AC respectively of the ΔABC. The four points A,B,D,E are concylic.
View SolutionIn the adjoining figure, O is the centre of the circle AC is a diameter and chord DE is parallel to the diameter AC. If ∠CBD=60∘ , find the value of ∠CDE
View SolutionIn the adjacent figure O is the centre of the circle. If ∠OAB=30∘,∠ABC=120∘,∠BCO=y∘and∠COA=x∘, then the find value sof x and y.
View SolutionIn a cyclic quadrilateral, the ratio of three consecutive angle is 1 : 2 : 3 Find the value of first and third angles.
View SolutionThe distance of the point from the centre of a circle with diameter of 16 cm is 17 cm. Then the length of the tangent from the point to the circle is
View SolutionIf I is the incenter of the circle inscribed in the triangle ABC and AI cuts BC at P, then
View SolutionIf P be a point in the interior of equilateral triangle ABC such that PA=3, PB=4andPC=5 then find a.
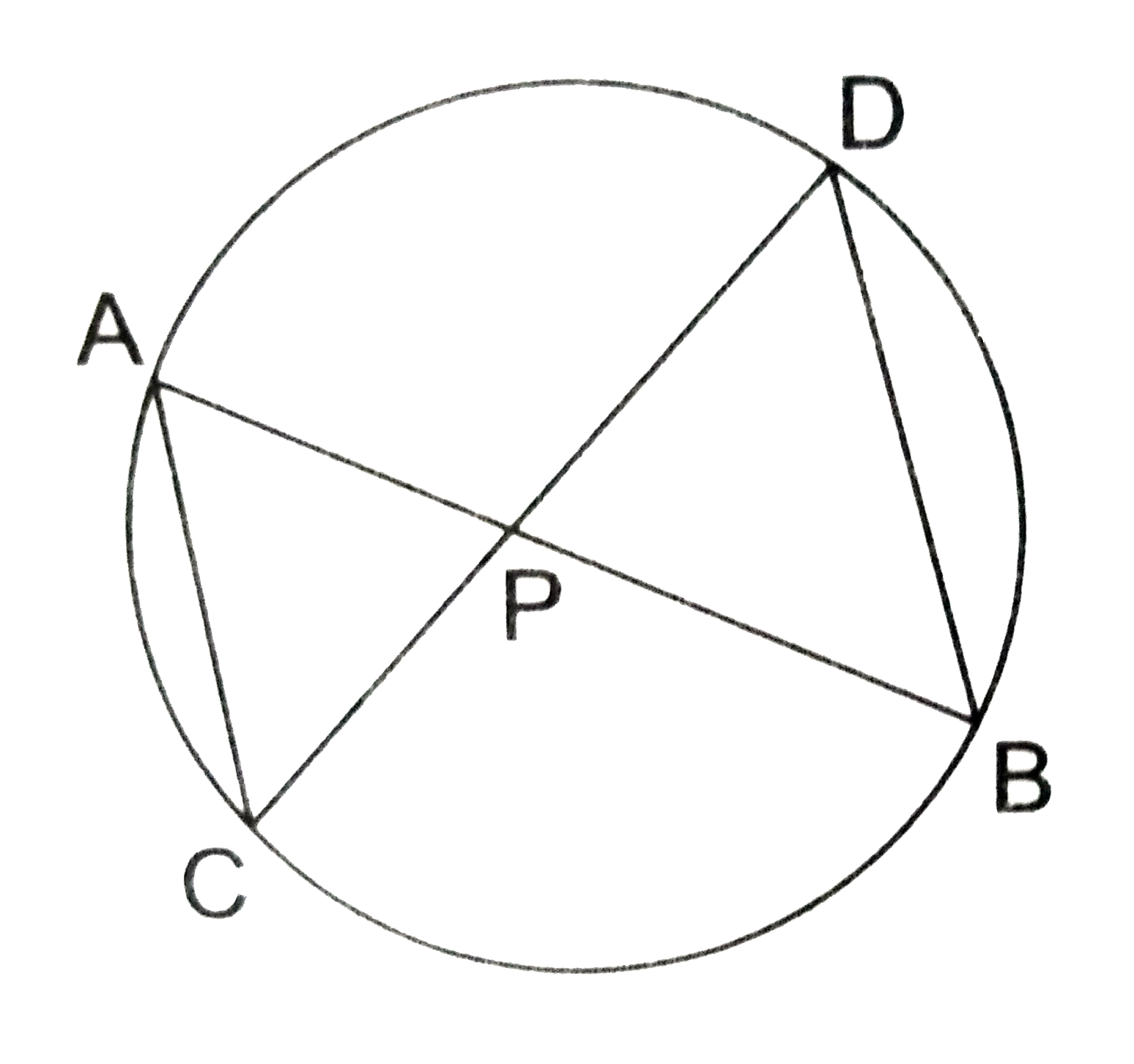
View SolutionIn a cricle, two chords AB and CD intersect at a point P inside the circle. Prove that
(a)ΔPAC~ΔPDB (b)PA⋅PB=PC⋅PD.
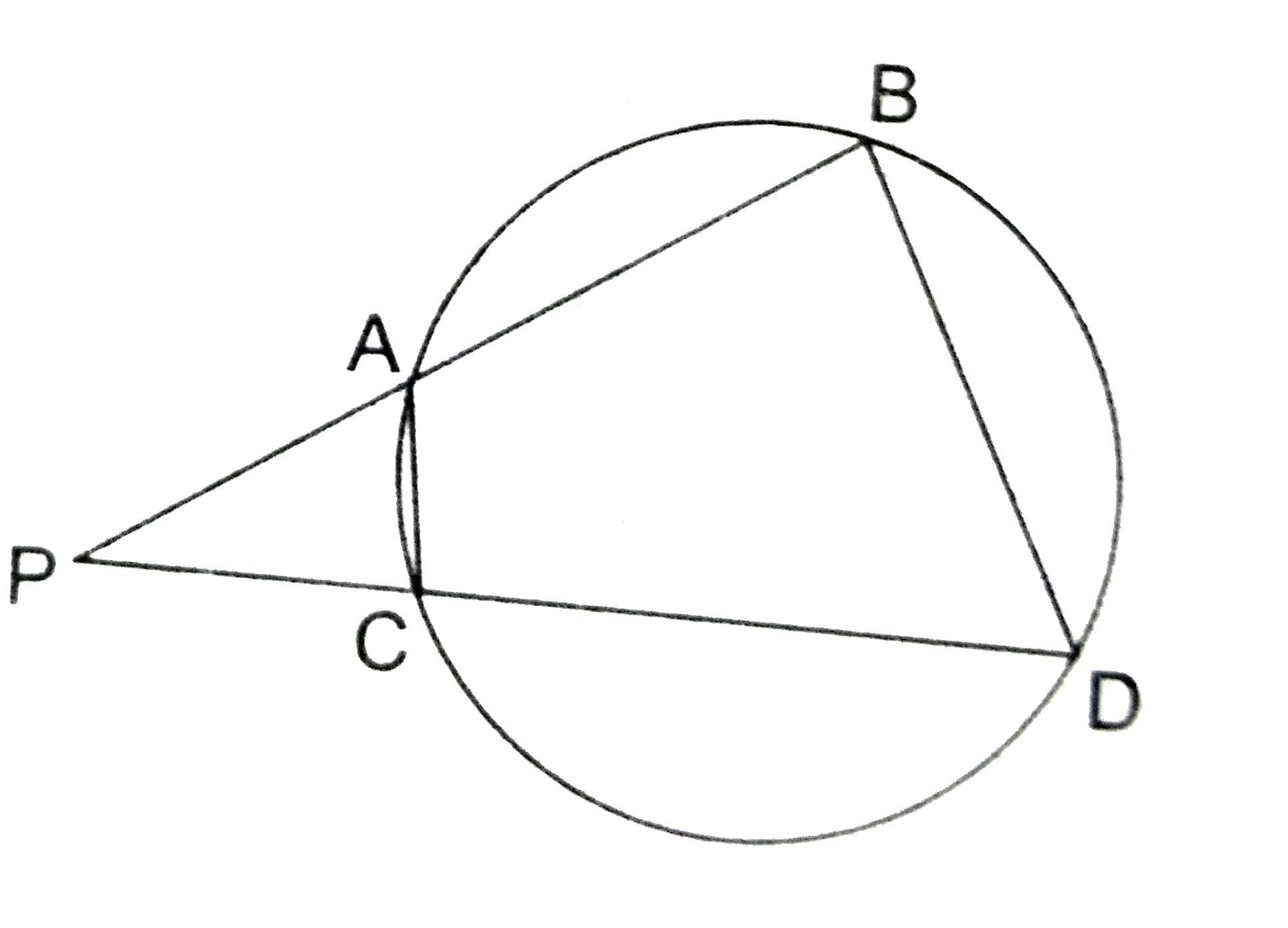
View SolutionTwo chords AB and CD of a circle intersect at a point outside the circle. Prove that
(a)ΔPAC~ΔPDB (b)PA⋅PB=PC⋅PD.
View SolutionABC is an equilateral triangle where AB = a and P is any point in its plane such that PA = PB + PC. Then PA2+PB2+PC2a2 is
View SolutionThe equilateral triangle ABC is inscribed in a circle. If P is any point on the ar BC, then prove that AB=PB+PC.
View Solutionत्रिभुज ABC में कोण B और C के समद्विभाजक बिंदु O पर काटते है|यदि बढ़ा हुआ AO भुजा BC को P पर काटता हो, तो सिद्ध करो की :
ABAC=BPPC
View SolutionIf P is a point on the plane of ΔABC such that ¯¯¯¯¯¯PA+¯¯¯¯¯¯PB+¯¯¯¯¯¯PC=0, then, for Δ ABC, the point P is
View SolutionI is the incentre of ΔABC, Produced AI bisects BC at D. Prove that ΔABC is isosceles.
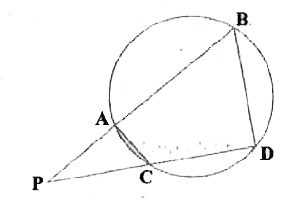
View SolutionIn Fig. two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that (i) ΔPAC~ΔPDB , (ii) PA . PB = PC . PD
View Solution
