If (a, 3a) is a variable point lying above the straight line 2x+y+4 =0 and below the line x+4y-8=0, then find the values of a. Solution in Bengali

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $- 4 / 5 < a < 8 / 13$

We have lines
$2 x + y + 4 = 0 (1)$
$and x + 4 y - 8 = 0 (2)$
Lines are drawn as shown in the following figure.

$Let L_{1} (x, y) = 2 x + y + 4$
$and L_{2} (x, y) = x + 4 y - 8$
$L_{1} (0, 0) = 4 > 0$
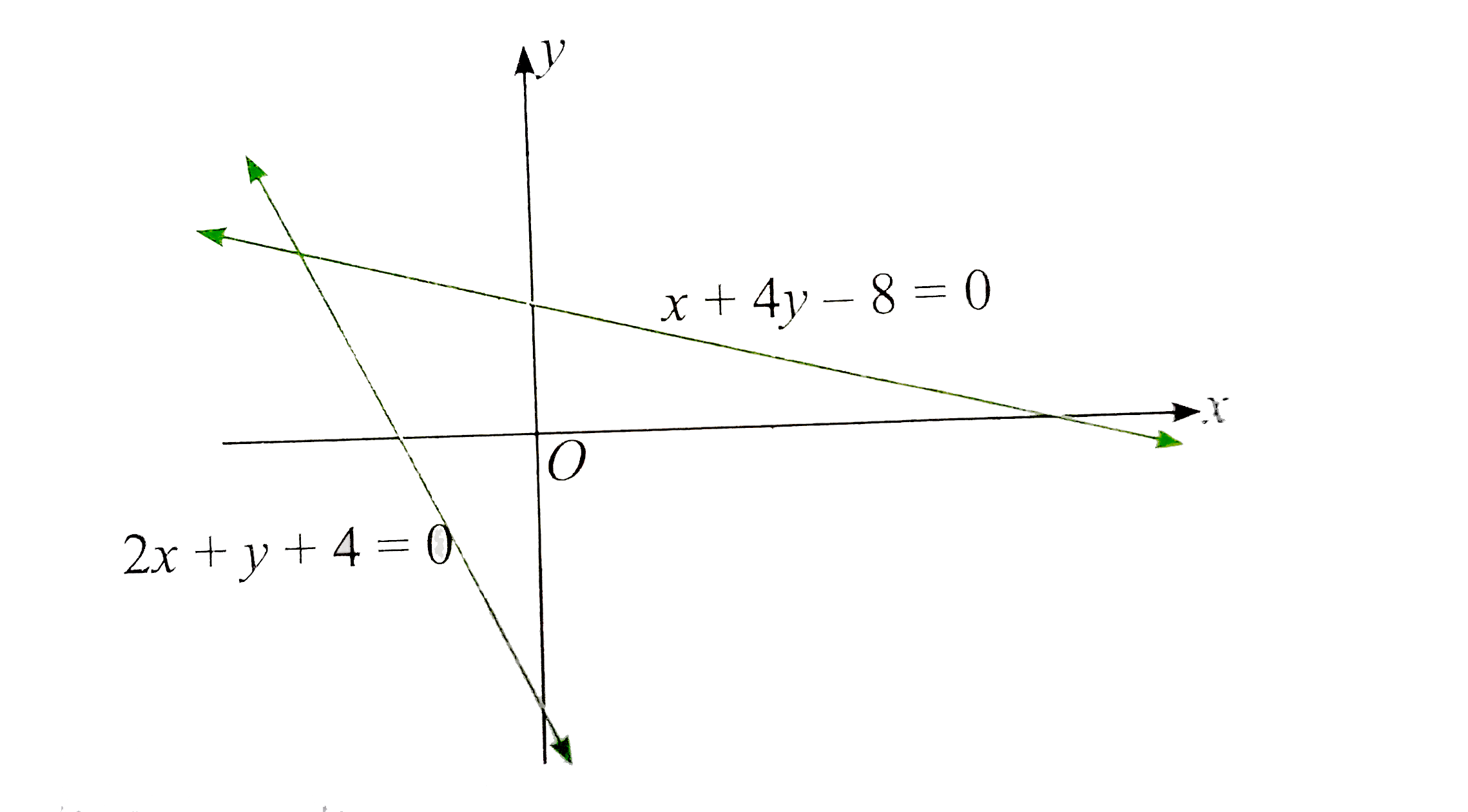
So, (a,3a) lies above the first line if
$L_{1} (a, 3 a) = 2 a + 3 a + 4 > 0$
$or a > - 4 / 5 (3)$
$L_{2} (0, 0) = - 8 < 0$
So, (a,3a) lies below the second line if
$L_{2} (a, 3 a) = a + 12 a - 8 < 0$
$or a < 8 / 13 (4)$
From (3) and (4),
$- 4 / 5 < a < 8 / 13$

|

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

CENGAGE PUBLICATION-STRAIGHT LINES-CONCEPT APPLICATION EXERCISE 2.4

Home
Ask Doubt
Profile