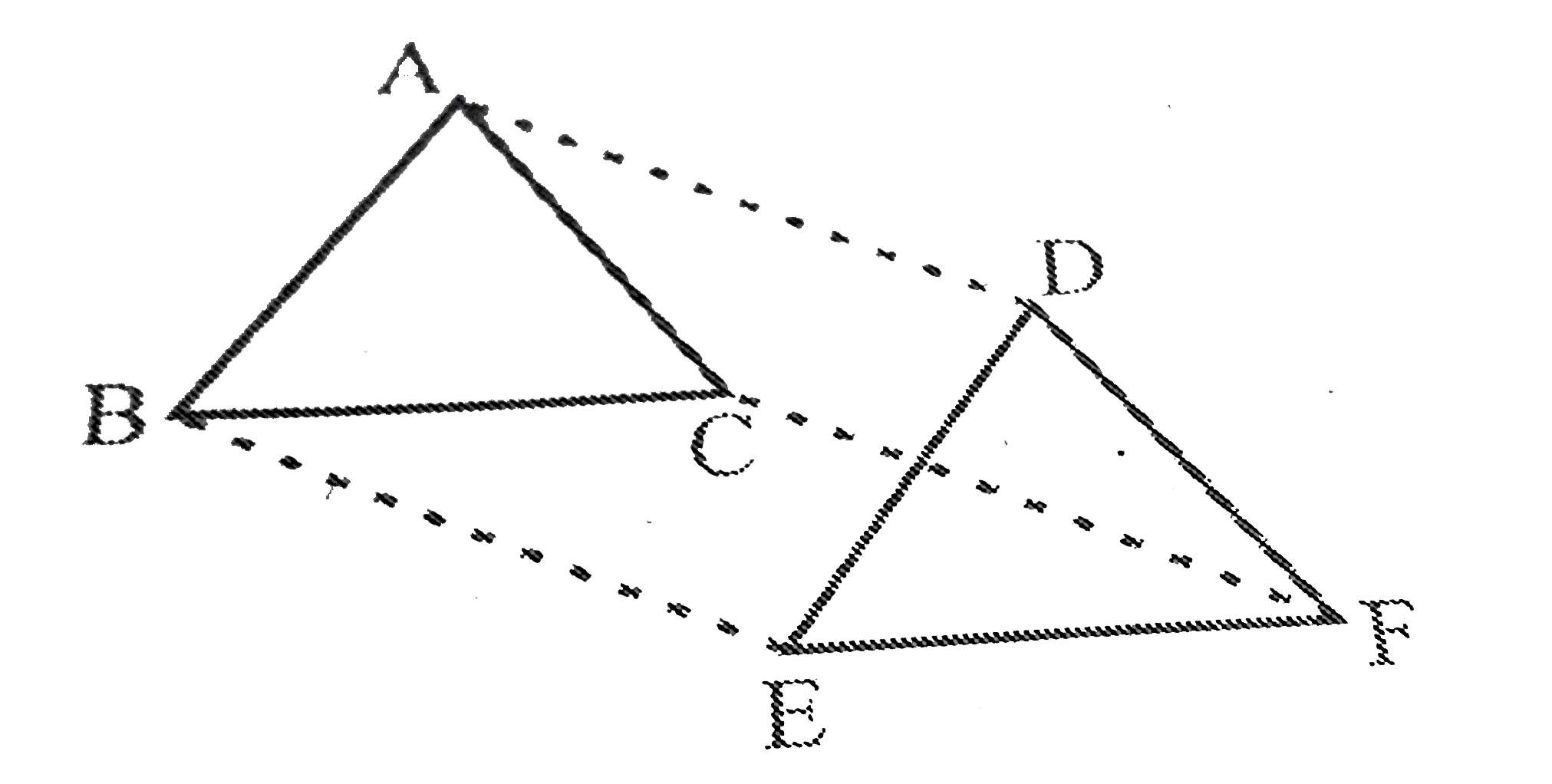
If ABC and DEF
are two triangles such
that AB, BC
are respectively equal
and parallel to DE, EF.
Then show that
(i) Quadrilateral ABED
is a parallelogram
(ii) Quadrilateral BCFE
is a parallelogram
(iii) AC=DF
(iv)
ABC ≅ DEF
Step by step video & image solution for If A B C\ a n d\ D E F are two triangles such that A B ,\ B C are respectively equal and parallel to D E ,\ E F. Then show that (i) Quadrilateral A B E D is a parallelogram (ii) Quadrilateral B C F E is a parallelogram (iii) A C=D F (iv) A B C\ ~=\ D E F by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
Similar Questions
If ABC and DEF are two triangles such that AB,BC are respectively equal and parallel to DE,EF, then show that (i) quad ABED is a parallelogram (ii) quad BCFE is a paralellogram (iii) AC=DF (iv) ΔABC≅ΔDEF
View SolutionIf ABC and DEF are similar triangles such that 2 AB=DE and BC=8cm , then EF=
View SolutionIn ΔABCand ΔDEF, AB = DE, AB ∣∣ DE, BC = EF and BC ∣∣ EF. Vertices A, B and C are joined to vertices D, E and F respectively (see Fig. 8.22).Show that
(i) quadrilateral ABED is a parallelogram
(ii) quadrilateral BEFC is a parallelogram
(iii) AD || CF and AD = CF
(iv) quadrilateral ACFD is a parallelogram
(v) AC = DF
(vi) ∆ ABC ≅ ∆ DEF.
 View Solution
View SolutionIf ABC and DEF are two triangles such that ABDE=BCEF=CAFD=25 , then Area(ABC):Area(DEF)=
View SolutionIf ABC and DEF are two triangles such that ABDE=BCEF=CAFD=34 , then write Area (ABC):Area(DEF) .
View SolutionIn Figure ABCD and AEFD are two parallelograms. Prove that: PE=FQ
View SolutionThe sides AB and CD of a parallelogram ABCD are bisected at EandF . Prove that EBFD is a parallelogram.
View SolutionE,F,G,H are respectively, the mid-points of the sides AB,BC,CD and DA of parallelogram ABCD . Show that the quadrilateral EFGH is a parallelogram and that its area is half the area of the parallelogram, ABCD.
View SolutionIn Figure, AB||CF and BC||ED . Prove that ∠ABC= ∠FDE
View SolutionIn Figure, ABCD is a parallelogram and EFCD is a rectangle. Also AL ⊥DC. Prove that
(i) ar(ABCD=ar(EFCD)
(ii) ar (ABCD)=DC x ALView Solution

