If A, B, C and D are four points such that ∠BAC=30∘and∠BDC=60∘,then D is the centre of the circle through A, B and C.
Because, there can be many points D, such that ∠BDC=60∘ and each such point cannot be the centre of the circle through, A, B and C.
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLARCHAPTER - CIRCLESEXERCISE - Exercise 10.4
2 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLARCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Areas Of Parallelograms And Triangles
34 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLARCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
If A, B, C and D are four points such that ∠BAC=45∘and∠BDC=45∘, then A, B, C and D are concyclic.
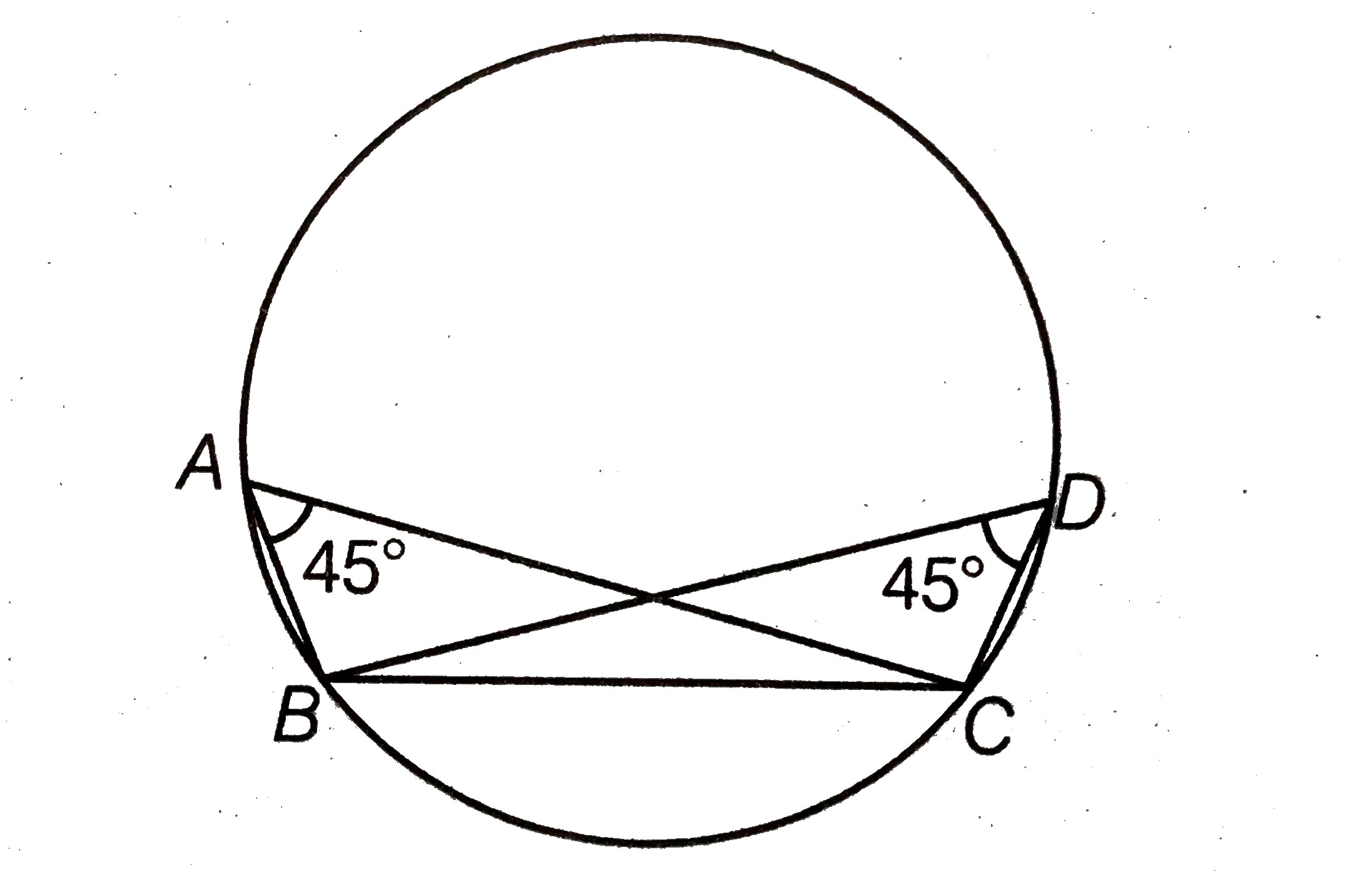
View SolutionIn figure, AB is a chord of the circle and AOC is the diameter such that ∠ACB=50∘. If AT is the tangent to the circle at the point A, then ∠BAT is equal to : (a) 45∘ , (b) 60∘ , (c) 50∘ , (d) 55∘
View Solution
Knowledge Check
If A, B, C and D are four numbers such that A:B=2:3,B:C=4:5,C:D=5:8, then A:D is equal to
A1:3B3:1C2:3D3:2If A, B, C and D are four numbers such that A : B = 2 : 3, B : C = 4 : 5, C : D = 5 : 8, then A : D is equal to
A1:3B3:1C2:3D3:2Two circles with centres P and Q intersect at B and C, A, D are points on the circles with centres P and Q respectively such that A, C, D are colliner. If ∠APB=130∘,and∠BQD=x∘, then the value of x is :
A65B130C195D135
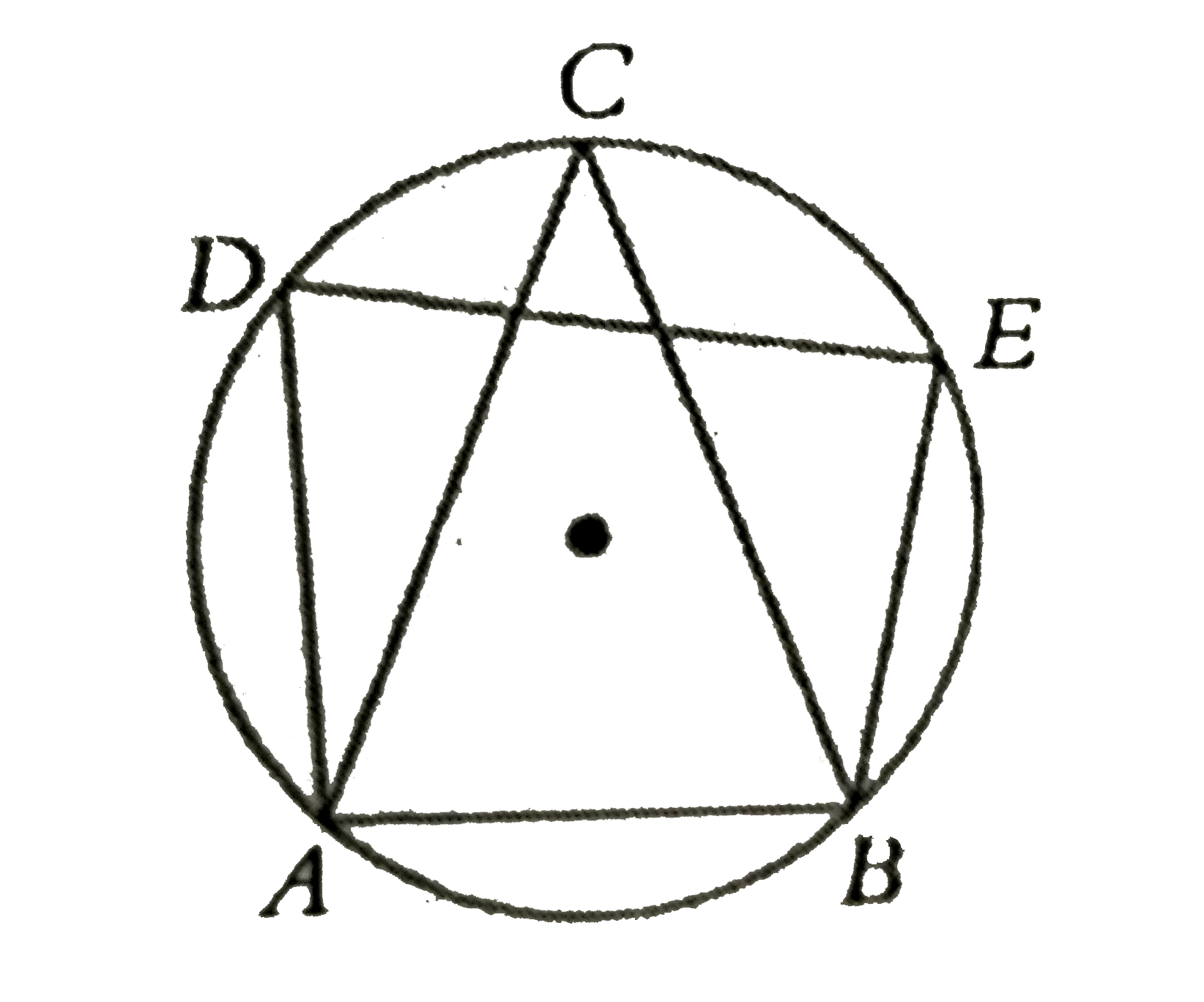
In the figure, A,B,E,C and D are the points on the circle. If AB=BE and ∠ACB=30∘ , then find ∠ADE.
View SolutionABCD is such a quadrilateral that A is the centre of the circle passing through B,CandD. Prove that ∠CBD+∠CDB=12∠BAD.
View SolutionO is the centre of the circle passing through the points A, B and C such that ∠BAO=30∘,∠BCO=40∘and∠AOC=x∘ . What is the value of x ?
View SolutionA,B,C and D are 4 points on the circumference of the circle and O is the centre of circle ∠OBD−∠CBD=∠BDC−∠ODB find ∠A
View SolutionPoints A,B,C and D are concyclic. BC is the diameter and O is the centre of the circle, ∠BAO=69∘ find ∠DAO+∠DCO
View Solution
