If A(3,4) and B(−5,−2) are the extremities of the base of an isosceles triangle ABC with tan C=2, then point C can be
(3√5−12,−(1+2√5))
⎛⎜ ⎜⎝−(3√5+5)2,3+2√5⎞⎟ ⎟⎠
(3√5−12,3−2√5)
⎛⎜ ⎜⎝−(3√5−5)2,−(1−2√5)⎞⎟ ⎟⎠
The correct Answer is:A, B
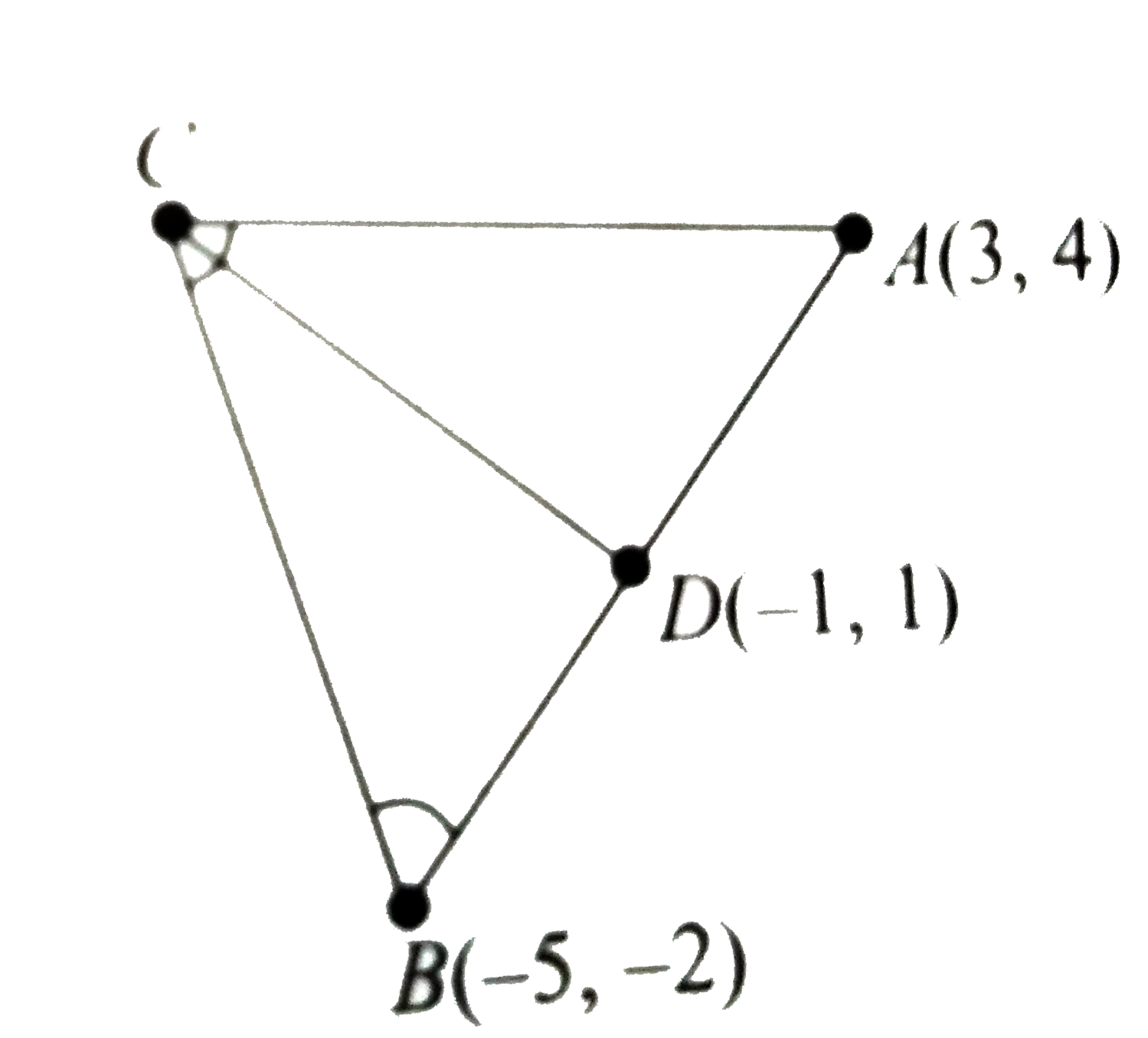
D(−1,1) is midpoint of AB.
CD=BDcot.C2=5.cot.C2
Now, tanC=2
⇒2tan.C21−tan−2.C2=2
⇒tan2.C2+tan.C2−1=0
⇒tan.C2=−1+√52
⇒cot.C2=√5+12
⇒CD=5(√5+12)=52(√5+1)
Slope of BD is 3/4.
∴ Slope of CD is −4/3=tanα
Using parametric form of straight line, coordinates of C are given by
⎛⎜
⎜⎝−1±5(√5+1)2cosα,1±5(√5+1)2sinα⎞⎟
⎟⎠
or (−5+3√52,2√5+3) and (3√5−12,−(2√5+1))
Topper's Solved these Questions
Similar Questions
If the extremities of the base of an isosceles triangle are the points (2a,0) and (0, a), and the equation of one of the side is x=2a, then the area of the triangle is (a)5a2sq.units (b) 5a22sq.units 25a22sq.units (d) none of these
View SolutionThe extremities of the base of an isosceles triangle ΔABC are the points A(2.0) and B(0,1). If the equation of the side AC is x=2 then the slope of the side BC
View Solution
Knowledge Check
If in a triangle ABC, b + c = 3a, then tan(B2)tan(C2) is equal to
A1/2B1/3C1/4D1/5
If A(-2,1),B(2,3) and C(-2,-4) be the vertices of a △ABC, show that tanB=23
View SolutionIf in a triangle ABC, b + c = 3a, then tan(B2)tan(C2) is equal to
View SolutionShow that the points A(7, 10), B(-2, 5) and C(3, -4) are the vertices of an isosceles right-angled triangle.
View SolutionShow that the points A(7, 10), B(-2, 5) and C(3, -4) are the vertices of an isosceles right-angled triangle.
View SolutionShow that the points A(7, 10), B(-2, 5) and C(3, -4) are the vertices of an isosceles right triangle.
View SolutionShow that the points A(7, 10), B(-2, 5) and C(3, -4) are the vertices of an isosceles right triangle.
View SolutionShow that the points A(7, 10), B(-2, 5) and C(3, -4) are the vertices of an isosceles right triangle.
View Solution
