ifA={(x,y):y=4x,x≠0}and
B={(x,y):x2+y2=8,x,y∈R},then
A∩B=ϕ
A∩B contains one point only
A∩Bcontains two points only
A∩B is a multiple of 4 points only .
The correct Answer is:C
To solve the problem, we need to find the intersection of the sets A and B defined as follows:
- Set A: A={(x,y):y=4x,x≠0}
- Set B: B={(x,y):x2+y2=8,x,y∈R}
Step 1: Substitute the equation of Set A into Set B
We know that y=4x from Set A. We will substitute this expression for y into the equation of Set B.
x2+(4x)2=8
Step 2: Simplify the equation
Now, we simplify the equation:
x2+16x2=8
Step 3: Multiply through by x2 to eliminate the fraction
To eliminate the fraction, multiply the entire equation by x2 (noting that x≠0):
x4+16=8x2
Step 4: Rearrange the equation
Rearranging gives us:
x4−8x2+16=0
Step 5: Let z=x2
Let z=x2. The equation becomes:
z2−8z+16=0
Step 6: Factor the quadratic equation
This can be factored as:
(z−4)2=0
Step 7: Solve for z
Setting the factor equal to zero gives:
z−4=0⟹z=4
Step 8: Substitute back to find x
Since z=x2:
x2=4⟹x=2 or x=−2
Step 9: Find corresponding y values
Now we substitute x back into the equation for y:
For x=2:
y=42=2
For x=−2:
y=4−2=−2
Step 10: Write the intersection points
Thus, the points of intersection A∩B are:
(2,2) and (−2,−2)
Final Result
The intersection of sets A and B contains the points (2,2) and (−2,−2).
---
- Set B: B={(x,y):x2+y2=8,x,y∈R}
y=42=2
y=4−2=−2
Topper's Solved these Questions
- SETSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SETSEXERCISE - Chapter Test
30 Videos
- SETSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SETSEXERCISE - Section I - Solved Mcqs
24 Videos
- SEQUENCES AND SERIESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Chapter Test
59 Videos
- STRAIGHT LINESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Chapter Test
34 Videos
Similar Questions
Knowledge Check
If R={(x,y):x,y∈N,x+2y=8} then range of R is
A{1, 2, 3, ... 7,8}B{1, 2, 3, ... 9, 10}C{1,3,5,7 ... 19}D{1,3,5,7, ... 15}
If A={(x, y):y=1x, 0≠x∈R}and B={(x,y):y=−x, x∈R} , then write A∩B.
View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
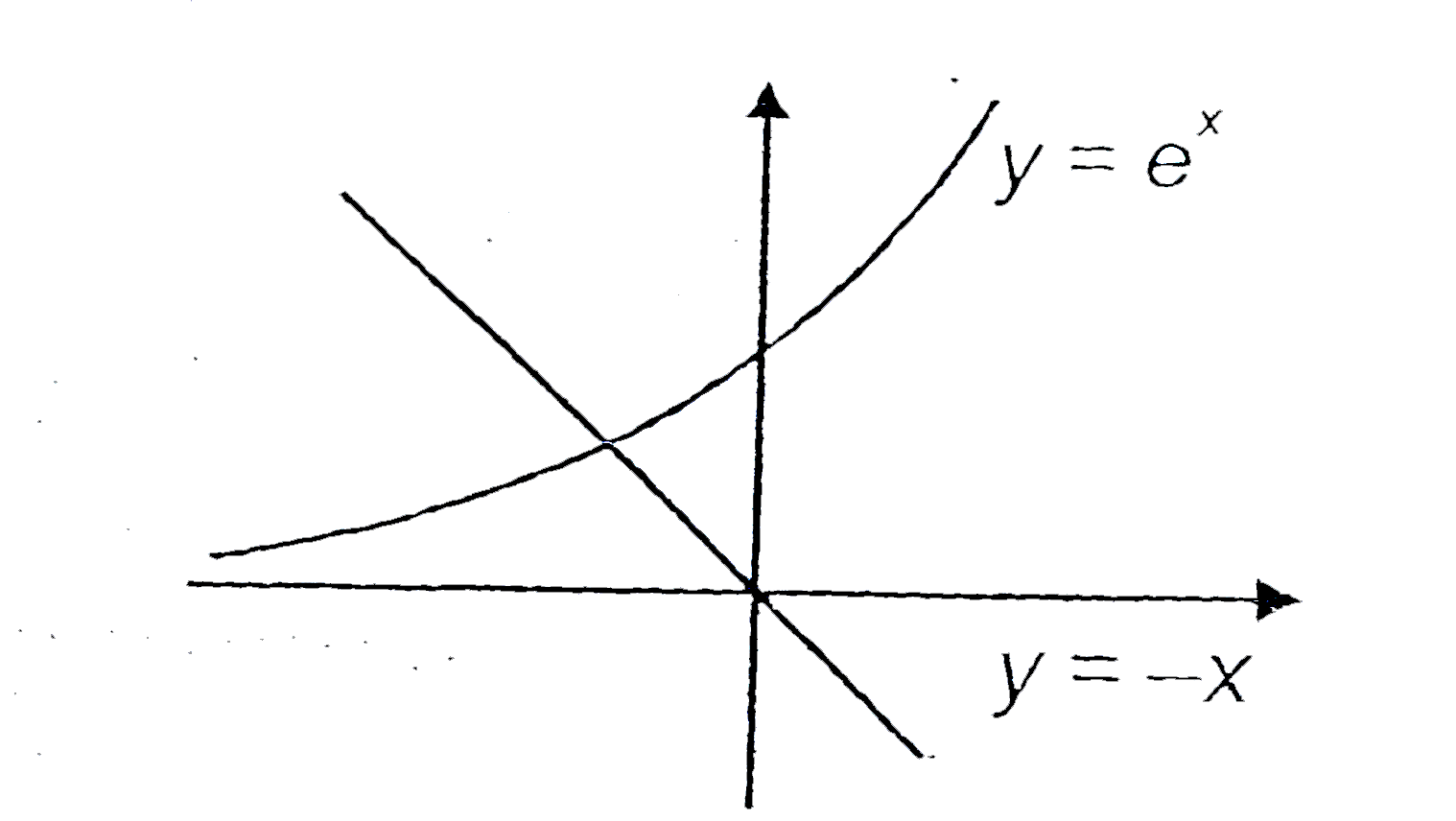
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A={(x,y):x2+y2≤2,x,y∈R}
B={{x,y):y≥x2,x,y∈R}
View SolutionifA={(x,y):x2+y2≤1,x,y∈R]and
B={(x,y):x2+y2≤x2+y2≤4,x,y∈R]then
View SolutionWhich of the following are function: {(x,y):y2=x,x,y∈R} b. {(x,y):y=|x|,x,y∈R} c. {(x,y):x2+y2=1,x,y∈R} d. {(x,y):x2−y2=1,x,y∈R}
View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
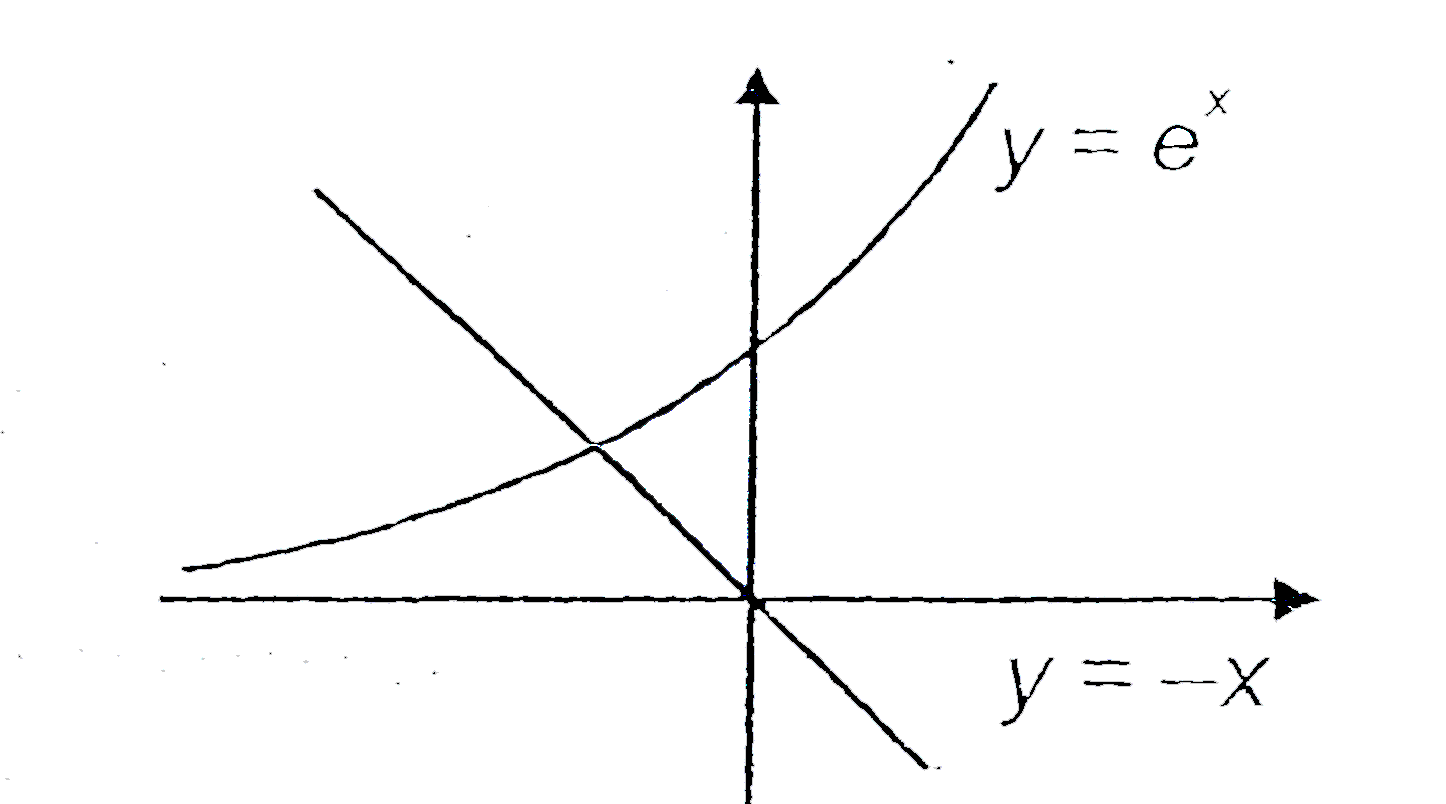
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A:{(x,y):y=√4−x2,x∈[−2,2]}
B={(x,y):y=|x|,x∈R}
Then n(A∩B)
View SolutionIf set A and B are defined as
A={(x,y)∣y=1x,0≠x∈R},B={(x,y)∣y=−x,x∈R,}. Then
View SolutionWhich one of the following is not a function? {(x,y):x,y∈R,x2=y} b. {(x,y):x,y∈R,y2=x} c. {(x,y):x,y∈R,x=y3} d. {(x,y):x,y∈R,y=x3}
View Solution
