in a class of 35 students , 17 have taken Mathematics , 10 have taken mathematics but not economics if each student has taken erither mathematics Of Economics or both , then the number of students who have taken Economics but not mathematics is
7
25
18
32
The correct Answer is:C
To solve the problem step by step, we will use the information provided and apply set theory concepts.
Step 1: Identify the given information
- Total number of students in the class (N) = 35
- Number of students who have taken Mathematics (n(M)) = 17
- Number of students who have taken Mathematics but not Economics (n(M - E)) = 10
Step 2: Use the relationship between sets
From the information given, we can determine the number of students who have taken both Mathematics and Economics (n(M ∩ E)).
Using the formula:
n(M)=n(M−E)+n(M∩E)
Substituting the known values:
17=10+n(M∩E)
Step 3: Solve for n(M ∩ E)
Rearranging the equation:
n(M∩E)=17−10
n(M∩E)=7
Step 4: Find the number of students who have taken Economics (n(E))
We know that all students have taken either Mathematics, Economics, or both. Therefore, we can use the formula for the union of two sets:
n(M∪E)=n(M)+n(E)−n(M∩E)
Given that n(M∪E)=35:
35=17+n(E)−7
Step 5: Solve for n(E)
Rearranging the equation:
n(E)=35−17+7
n(E)=25
Step 6: Find the number of students who have taken Economics but not Mathematics (n(E - M))
Using the formula:
n(E−M)=n(E)−n(M∩E)
Substituting the known values:
n(E−M)=25−7
n(E−M)=18
Final Answer
The number of students who have taken Economics but not Mathematics is 18.
---
- Total number of students in the class (N) = 35
- Number of students who have taken Mathematics (n(M)) = 17
- Number of students who have taken Mathematics but not Economics (n(M - E)) = 10
From the information given, we can determine the number of students who have taken both Mathematics and Economics (n(M ∩ E)).
n(M)=n(M−E)+n(M∩E)
Substituting the known values:
17=10+n(M∩E)
Rearranging the equation:
n(M∩E)=17−10
n(M∩E)=7
We know that all students have taken either Mathematics, Economics, or both. Therefore, we can use the formula for the union of two sets:
n(M∪E)=n(M)+n(E)−n(M∩E)
Given that n(M∪E)=35:
35=17+n(E)−7
Rearranging the equation:
n(E)=35−17+7
n(E)=25
Using the formula:
n(E−M)=n(E)−n(M∩E)
Substituting the known values:
n(E−M)=25−7
n(E−M)=18
The number of students who have taken Economics but not Mathematics is 18.
Topper's Solved these Questions
- SETSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SETSEXERCISE - Chapter Test
30 Videos
- SETSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SETSEXERCISE - Section I - Solved Mcqs
24 Videos
- SEQUENCES AND SERIESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Chapter Test
59 Videos
- STRAIGHT LINESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Chapter Test
34 Videos
Similar Questions
In a class of 60 students, 30 students like Mathematics, 25 like Science and 15 like both. Then, the number of students who like either Mathematics or Science is
View SolutionIf in a class there are 200 students in which 120 take Mathematics, 90 take Physics, 60 take Chemistry, 50 take Mathematics & Physics, 50 take Mathematics & Chemistry, 43 take Physics & Chemistry and 38 take Mathematics Physics & Chemistry, then the number of students who hace taken exactly one subject is
View SolutionIn a class of 35 students, 18 students opt Maths, 12 students opt Maths but not Science. Find the number of students who opt both subjects. Also find the number of students who opt Science but not Maths. It is given that each student opt atleast one subject.
View SolutionFrom the details given below, calculate the five yearly moving averages of the number of students who have studied in a school.
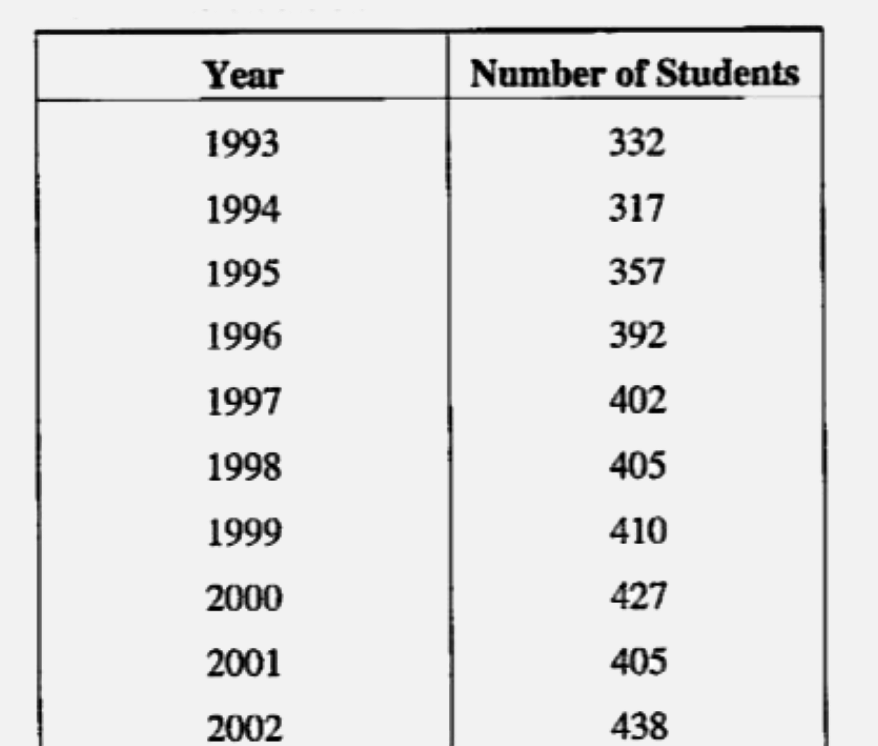
View SolutionIn a class of 55 students the number of students studying subjects are , 23 iin Mathematics 24.in physics 19in chemisty 12 in Mathematics and physics ,9 in Mathematics and chemistry ,7 in physics and chemistry and 4 in all the three subjects.
the number of students who have taken ecactly one subject is
View SolutionIn a class of 125 students 70 passed in Mathematics, 55 in statistics, and 30 in both. Then find the probability that a student selected at random from the class has passed in only one subject.
View SolutionIn a class of 125 students 70 passed in Mathematics, 55 in statistics, and 30 in both. Then find the probability that a student selected at random from the class has passes in only one subject.
View SolutionCalculate five yearly moving average of the number of students of who have studied in a school given below.

View SolutionTen students of class X took part in Mathematics quiz. If the number of girls is 4 more than the number of boys. Represent this situation algebraically.
View SolutionIn a class of 55 students, the number of students studying different subjects are 23 in Mathematics, 24 in Physics, 19 in Chemistry, 12 in Mathematics and Physics, 9 in Mathematics and Chemistry, 7 in Physics and Chemistry and 4 in all the three subjects. Find the number of students who have taken exactly one subject.
View Solution
