Question

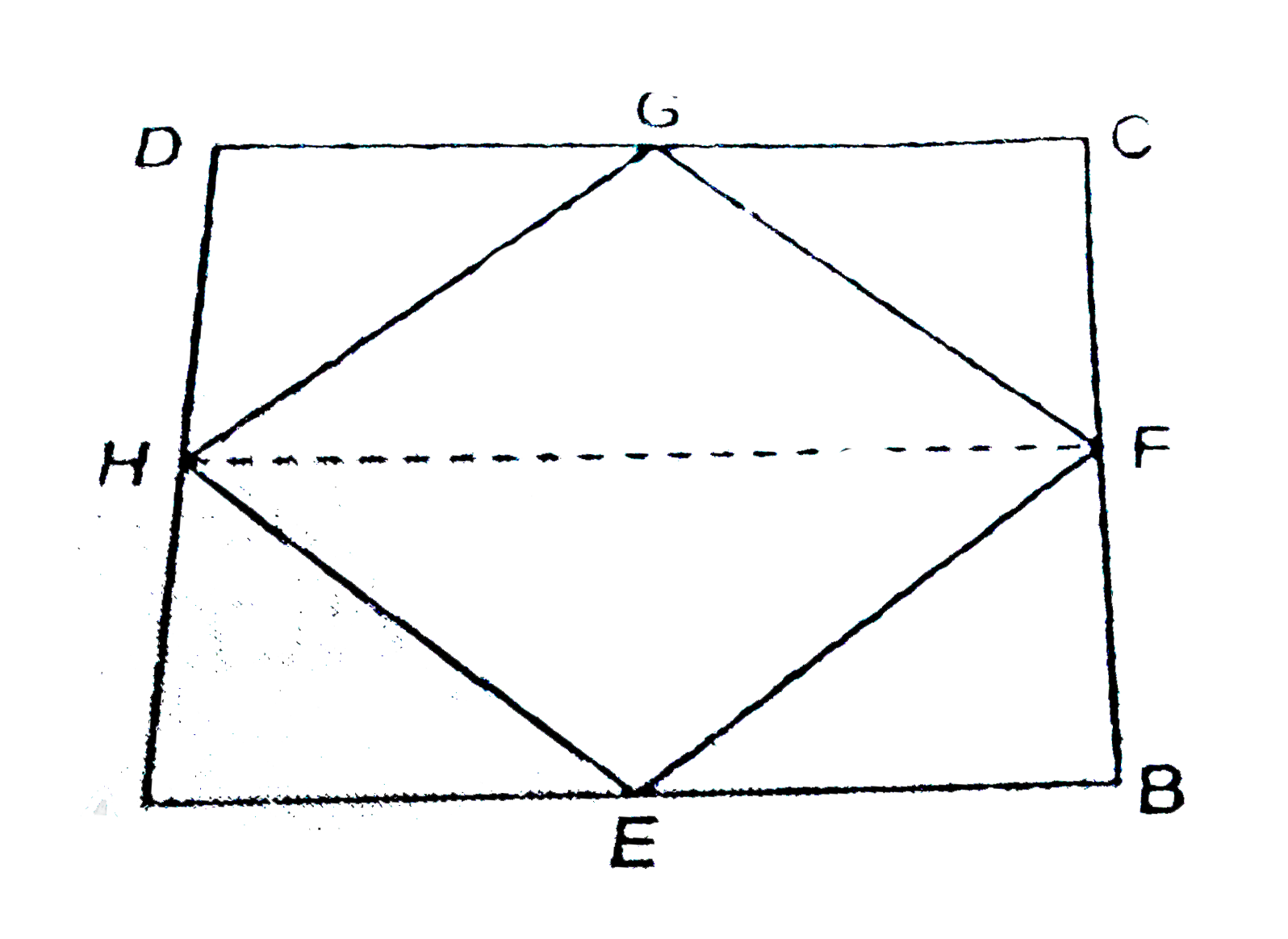
If $E,F,GandH$
are
respectively the mid-points of the sides of a parallelogram $ABCD,$
Show that $ar\left(EFGH\right)=\frac{1}{2}ar\left(ABCD\right)$

Explanation

Given, E, F, G and H are respectively the mid-points of the sides AB, BC, CD and AD. Joint if, it will parallel to CD and AB.
Now, parallelogram HDCF and triangle HGF stand on the same base HF and lie between the same parallel lines DC and HF.
`:. ar(DeltaHGF) = (1)/(2) ar(HDCF)`...(1)
Similarly, parallelogram ABFH and triangle HEF stand on the same base HF and lie between the same parallel lines HF and AB.
`ar(DeltaHEF) = (1)/(2) ar(ABFH)`...(2)
On adding (1) and (2), we get
`ar(DeltaHGF) + ar(DeltaHEF) = (1)/(2) [ar(HDCF) + ar(ABFH)]`
`rArr ar(EFGH) = (1)/(2) ar(ABCD)`