ABCD is a square. E and F are respectively the mid-points of BC and CD. If R is the mid-point of EF, prove that ar(ΔAER)=ar(ΔAFR).

In ΔABEandΔADF,
∵∵∵⎧⎪⎨⎪⎩AB=AD(sides of a square are equal)∠ABE=∠ADF(each90∘) BE=DF
( ∵ E is the mid-point of BC and F is the mid-poiunt of CD. Also, 12BC=12CD)
∴ΔABE≅ΔADF (by SAS congruence rule)
∴AE=AF (c.p.c.t)...(1)
Now, in ΔAERandΔAFR,
∵⎧⎪⎨⎪⎩AE=AF [from(1)]ER=RF(∵R is mid-point of EF)AR=AR(common side)
∴ΔAER=ΔAFR (by SSS rule of congruence)
Hence, ar(ΔAER)=ar(ΔAFR) ( ∵ congruent triangle are equal in area)
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Exercise34videos
AREA OF PARALLELOGRAMS AND TRIANGLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (very Short Answer Questions)10videos
AREA OF PARALLELOGRAMS AND TRIANGLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)5videos
AREA OF PARALLELOGRAMS AND TRIANGLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Revision Exercise (long Answer Questions )5videos
CIRCLE
Similar Questions
If D, E and F are respectively, the mid-points of AB, AC and BC in ΔABC, then BE + AF is equal to
View SolutionABCD is a square, X is the mid-point of AB and Y the mid-point of BC. Prove that
∠DXA=∠AYBView SolutionABCD is a square, X is the mid-point of AB and Y the mid-point of BC. Prove that
the triangles ADX and BAY are congruent.View SolutionABCD is a square, X is the mid-point of AB and Y the mid-point of BC. Prove that
DX is perpendicular to AY.View SolutionD is the mid-point of side AB of the triangle ABC.E is the mid-point of CD and F is the mid-point of AE. Prove that 8× area of (ΔAFD)= area of ΔABC
View SolutionThe following figure shows a triangle ABC in which P, Q and R are mid-points of sides AB, BC and CA respectively. S is mid-point of PO.
Prove that : ar.(ΔABC)=8×ar.(ΔQSB)
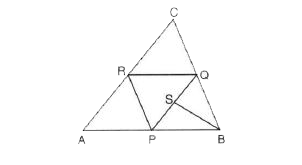 View Solution
View SolutionABC is a triangle in which D is the mid-point of BC and E is the mid-point of AD. Prove that area of △BED=14area of△ABC. GIVEN : A △ABC,D is the mid-point of BC and E is the mid-point of the median AD. TO PROVE : ar(△BED)=14ar(△ABC).
View SolutionD is the mid-point of side BC of △ABC and E is the mid-point of BD. If O is the mid-point of AE , prove that ar(△BOE)=18ar(△ABC).
View SolutionIn parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
View SolutionD, E and F are respectively the mid-points of sides AB. BC and CA of △ABC. Find the ratio of the areas of △DEF and △ABC.
View Solution

