In the figure, PSDA is a parallelogram. Points Q and R are taken on PS such that PQ=QR=RS and PA||QB||RC. Prove that ar(PQE)=ar(CFD).
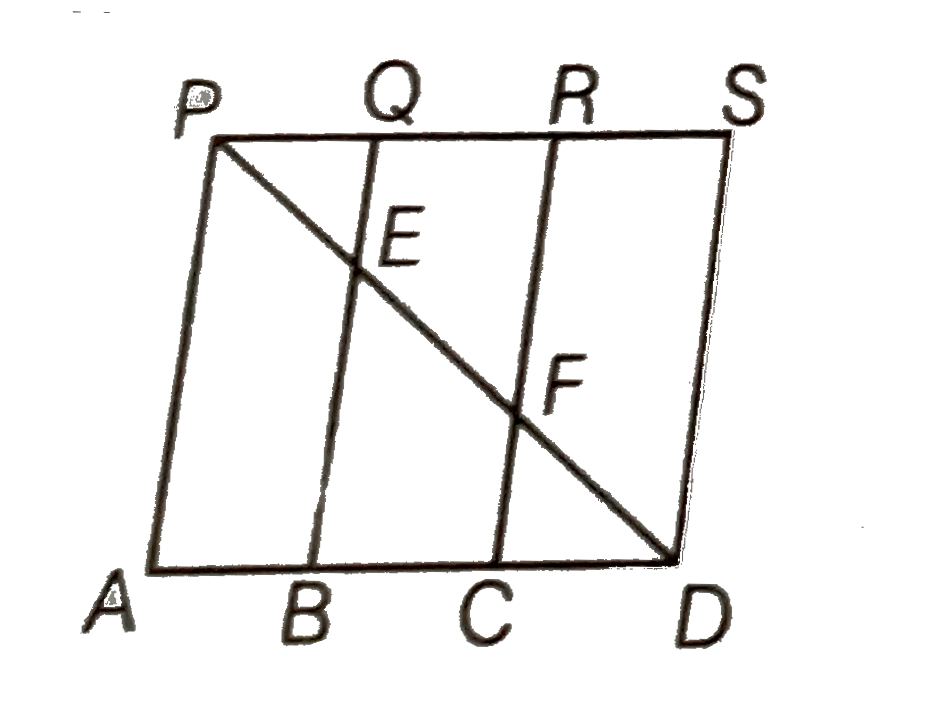
Given : PSDA is a parallelogram. Points Q and R are taken on PS such that PQ=QR=RSandPA||QB||RC.
To prove : ar(ΔPQE)=ar(ΔCFD)
Proof: Now, PS=AD (opposite side of a parallelogram)
∴13PS=13AD⇒PQ=CD...(1)
Again, PS∣∣AD and QB cut them.
∴∠PQE=∠CBE (alternate angles)...(2)
Now, QB∣∣RC and AD cuts them
∴∠QBD=∠RCD (corresponding angles)...(3)
So, ∠PQE=∠FCD...(4)
[from (2) and (3), ∠CBEand∠QBD are same and ∠RCDand∠FCD are same] ΔPQEandΔCFD
∵⎧⎪⎨⎪⎩∠QPE=∠CDF (alternate angles) PQ=CD [from(1)]∠PQE=∠FCD [from (4)]
∴ΔPQE≅ΔCFD (by ASA congruence rule)
Hence, ar(ΔPQE)=ar(ΔCFD) (congruent triangles are equal in area)
Topper's Solved these Questions
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Exercise
34 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (very Short Answer Questions)
10 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CIRCLE BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Revision Exercise (long Answer Questions )
5 Videos
Similar Questions
In the given figure, QR is parallel to AB and DR is parallel to QB.
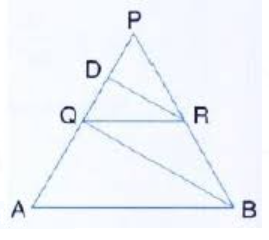
Prove that : PQ2=PD×PA.
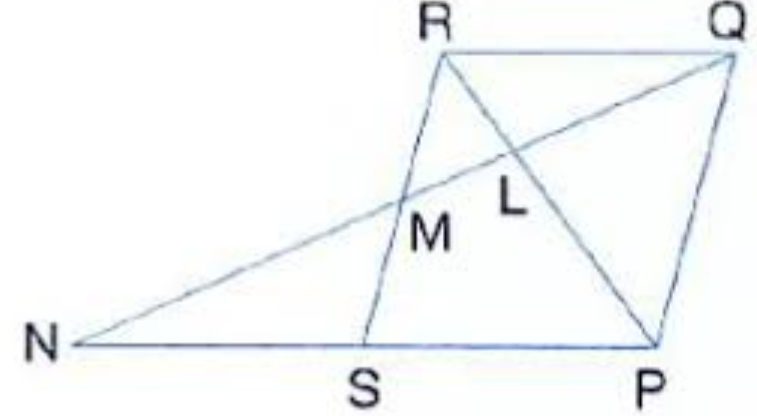
View SolutionIn the figure, PQRS is a parallelogram with PQ = 16 cm and QR = 10 cm. L is a point on PR such that RL:LP=2:3. QL produced meets RS at M and PS produced at N.
Find the lengths of PN and RM.
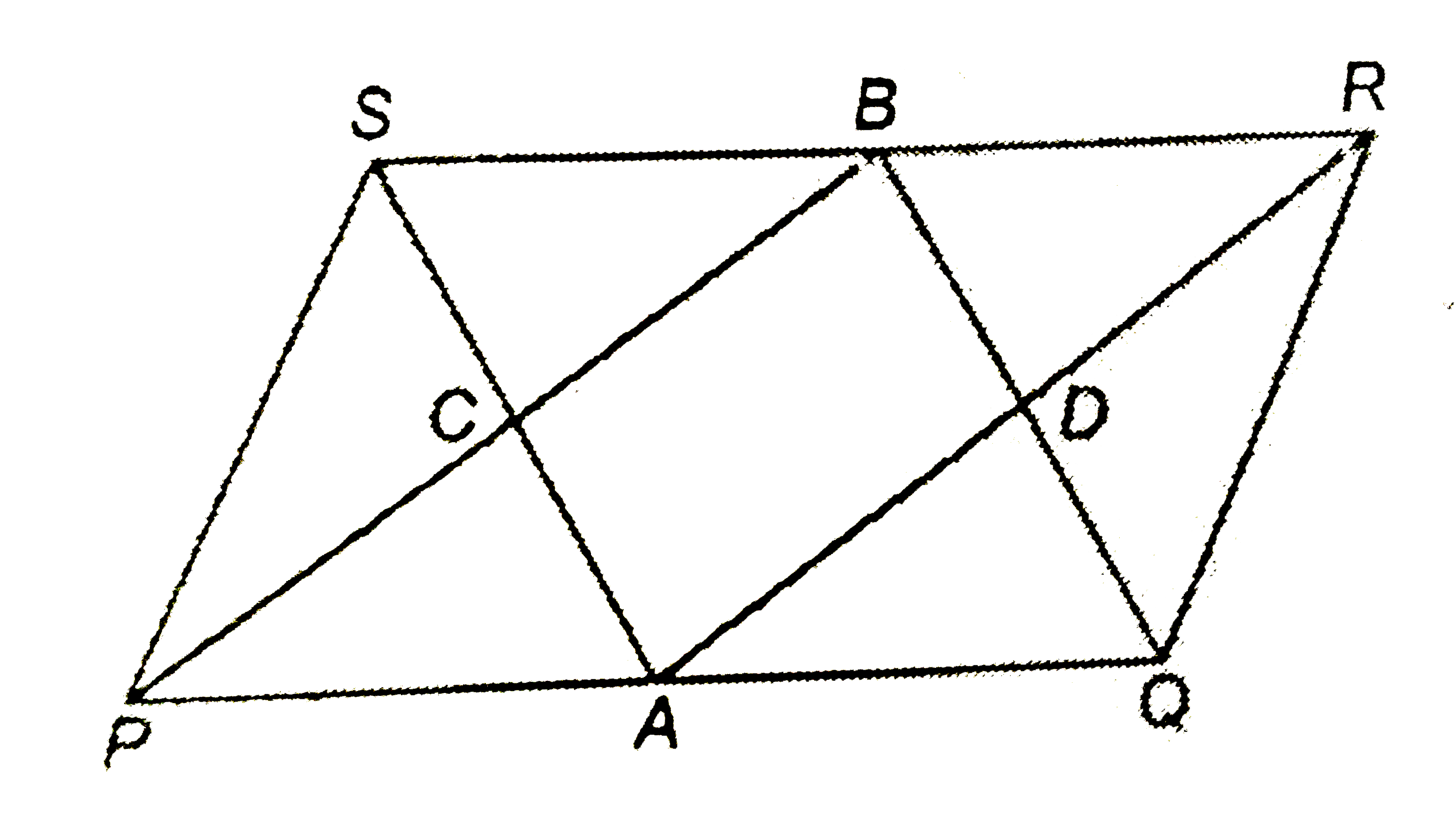
View SolutionIn the adjoining figure, PQRS is a parallelogram. A and B are the mid-points of PQ of SR respectively. If PS= BR, then prove that quadrilateral ADBC is a reactangle.
View SolutionP is the mid-point of the side CD of a parallelogram ABCD. A line through C parallel to PA intersects AB at Q and DA produced at R. Prove that DA = AR and CQ = QR.
View SolutionIf Q is a point on the side SR of a triangle ΔPSR such that PQ=PR then prove that PS>PQ
View SolutionABCD is a square. P, Q and Rare the points on AB, BC and CD respectively, such that AP = BQ = CR. Prove that:
PQ = QR
View SolutionIn Figure, ABCD is a parallelogram. Prove that: ar(BCP)=ar(DPQ) CONSTRUCTION : Join AC.
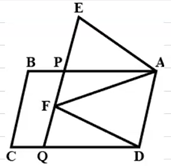
View SolutionIn figure, ABCD and AEFD are two parallelograms. Prove that ar(ΔPEA)=ar(ΔQFD).
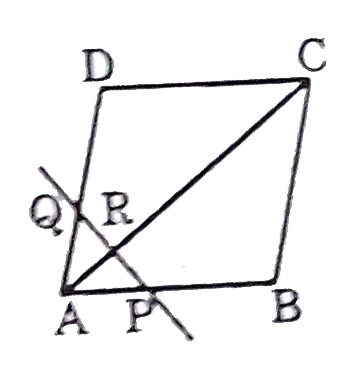
View SolutionA transversal cuts side AB and AD and diagonal AC of parallelogram ABCD in points P,Q and R respectively such that AP: PB =1 :2 and AQ: QD=2:3 . Find the ratio AR : RC
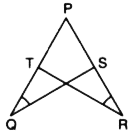
View SolutionThe given figure shows PQ=PRand∠Q=∠R.
Prove that ΔPQS=ΔPRT
View Solution
