If from an external point P of a circle with centre O, two tangents PQ and PR are drawn such ∠QPR=120∘, prove that 2PQ=PO.

In ΔOPQ, we have
∠PQO=90∘ [∵ the tangent at any point is perpendicular to the radius through the point of contact]
and ∠QPO=12×∠QPR=12×120∘=60∘. [∵ the two tangents drawn from an external point are equally inclined to the line segment joining the centre to that point and so ∠QPO=∠RPO]
In right ΔOPQ, we have
cos(∠QPO)=PQPO
⇒cos60∘=PQPO⇒12=PQPO=2PQ=PO.
Topper's Solved these Questions
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Exercise 8A
16 Videos
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Exercise 8B
15 Videos
- ARITHMETIC PROGRESSIONBOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)
30 Videos
- CONSTRUCTIONSBOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - Test Yourself
10 Videos
Similar Questions
Knowledge Check
In the given figure tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPO=30∘. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
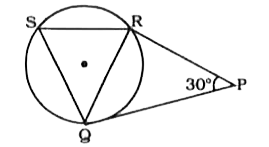 A30∘B50∘C45∘D60∘
A30∘B50∘C45∘D60∘2 equal tangents PA and PB are drawn from an external point P on a circle with centre O. What is the length of each tangent, if P Is 12 cm from the centre and the angle between the tangents is 120∘ ?
A24 cm.B6 cm.C8 cm.DCannot be determined
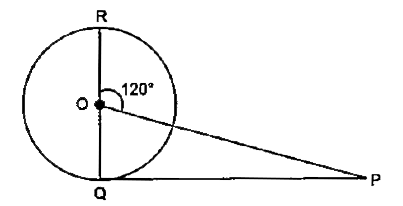
In Fig. two tangents RQ and RP are drawn from an external point R to the circle with centre O. If ∠PRQ=120∘ , then prove that OR = PR + RQ .
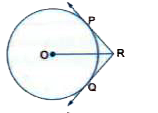
View SolutionPQ is a tangent drawn from an external point P to a circle with center O, ∠QOR is the diameter of the circle. If ∠POR=120∘. What is the measure of ∠OPQ?
View SolutionIn Fig, PQ is a tangent from an external point P to a circle with centre O and OP cuts the circle at T and QOR is a diameter. If ∠POR=130∘ and S is a point on the circle, find ∠1+∠2.
View SolutionFrom a point P, two tangents PT and PS are drawn to a circle with center O.Such that ∠SPT=120∘. Prove that OP=2PS.
View SolutionTwo tangents PAandPB are drawn from an external point P to a circle with centre O. Prove that AOBP is a cyclic quadrilateral.
View SolutionIn the figure , PQ and PR are tangents drawn from and external point P to the circle with centre O. Q and R are the points of contact. If PQ = 5 cm then what is the length of segment PR ? Why ?

View Solution
