Two tangents PAandPB are drawn from an external point P to a circle with centre O. Prove that AOBP is a cyclic quadrilateral.
PA and PB are tangents to the circle
∴OA⊥PAandOB⊥PB(tangent to the circle is perpendicular to radius at the of contact)
∴∠Aand∠Bare900
In quadrilateral AOBP
∠A+∠O+∠B+∠P=360
0
∴900+∠O+900+∠P=360
^0
∴∠O+∠P=1800
Sum of opposite angles of quadrilateral AOBPis1800
Hence, quadrilateral AOBP is cyclic quadrilateral
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPO=30∘. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
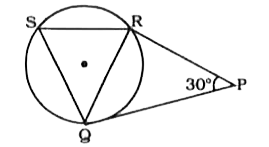 A30∘B50∘C45∘D60∘
A30∘B50∘C45∘D60∘ - Question 2 - Select One
2 equal tangents PA and PB are drawn from an external point P on a circle with centre O. What is the length of each tangent, if P Is 12 cm from the centre and the angle between the tangents is 120∘ ?
A24 cm.B6 cm.C8 cm.DCannot be determined
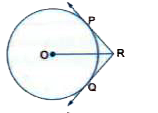
In Fig. two tangents RQ and RP are drawn from an external point R to the circle with centre O. If ∠PRQ=120∘ , then prove that OR = PR + RQ .
 View Solution
View SolutionTwo tangents TP and TQ are drawn to a circle with centre O from an external point T . Prove that ∠PTQ=2∠OPQ .
View SolutionTwo tangents PA and PB are drawn to a circle with centre O from an external point P. Prove that ∠APB=2∠OAB
 View Solution
View SolutionIn Fig. 10.60, PA and PB are tangents from an external point P to a circle with centre O . LN touches the circle at M . Prove that PL+LM=PN+MN . (FIGURE)
View SolutionIn the figure, PA is a tangent from an external point P to a circle with centre O. If ∠POB=115∘, find ∠APO.
 View Solution
View SolutionIn figure, PTandPS are tangents drawn from a point P to a circle with centre at 0. If ∠OPT=35∘, find aandb.
View Solution

