If from any point on the common chord of two intersecting circles, tangents be drawn to the circles, prove that they are equal.
To prove that the lengths of the tangents drawn from a point on the common chord of two intersecting circles to the circles are equal, we can follow these steps:
1. Identify the Circles and Points:
Let the two circles intersect at point M. Let O be a point on the common chord of the two circles.
2. Draw Tangents:
From point O, draw tangents OP to the first circle and OQ to the second circle.
3. Use the Tangent-Secant Theorem:
According to the tangent-secant theorem, for any point outside a circle, the square of the length of the tangent segment from that point to the circle is equal to the product of the lengths of the entire secant segment and its external segment.
- For the first circle, if OM is the distance from point O to the intersection point M on the first circle, then:
OP2=OM⋅ON
where N is the other intersection point of the secant line through O.
4. Apply the Same for the Second Circle:
Similarly, for the second circle, we have:
OQ2=OM⋅OM′
where M′ is the intersection point on the second circle.
5. Equate the Two Expressions:
Since both OP2 and OQ2 are equal to the same product involving OM, we can write:
OP2=OQ2
6. Conclude that the Tangents are Equal:
Taking the square root of both sides gives:
OP=OQ
Thus, the lengths of the tangents from point O to the two circles are equal.
Let the two circles intersect at point M. Let O be a point on the common chord of the two circles.
From point O, draw tangents OP to the first circle and OQ to the second circle.
According to the tangent-secant theorem, for any point outside a circle, the square of the length of the tangent segment from that point to the circle is equal to the product of the lengths of the entire secant segment and its external segment.
- For the first circle, if OM is the distance from point O to the intersection point M on the first circle, then:
OP2=OM⋅ON
where N is the other intersection point of the secant line through O.
Similarly, for the second circle, we have:
OQ2=OM⋅OM′
where M′ is the intersection point on the second circle.
Since both OP2 and OQ2 are equal to the same product involving OM, we can write:
OP2=OQ2
Taking the square root of both sides gives:
OP=OQ
Thus, the lengths of the tangents from point O to the two circles are equal.
Topper's Solved these Questions
Similar Questions
In the given figure, MN is the common chord of two intersecting circles and AB is their common tangent.
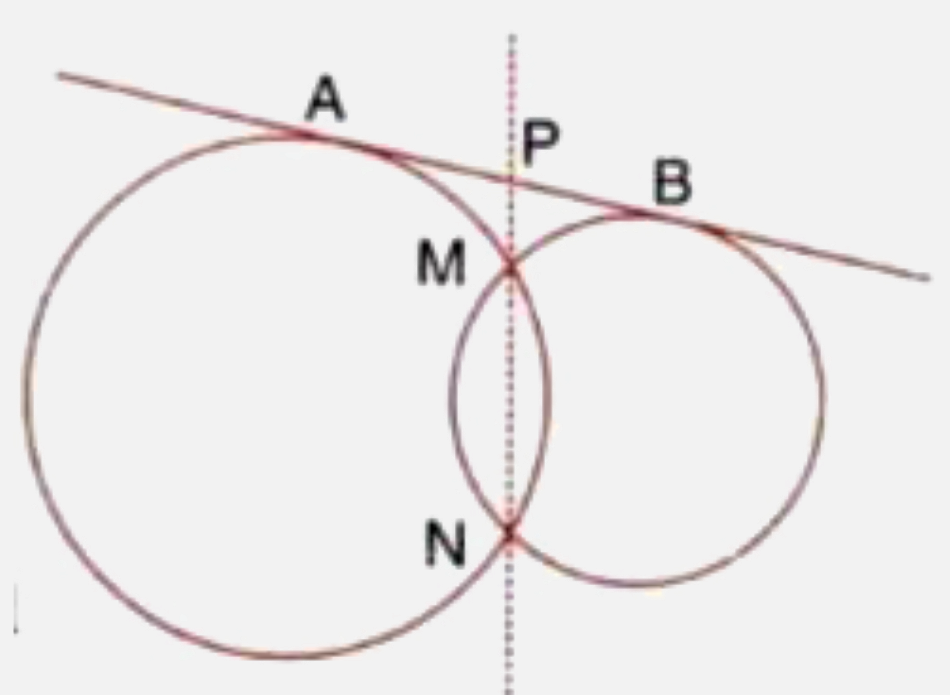
Prove that the line NM produced bisects AB at P.View SolutionA chord PQ of a circle is parallel to the tangent drawn at a point R of the circle,Prove that R bisects the arc PRQ.
View SolutionProve that the length of the tangents drawn from an external point to a circle are equal.
View SolutionProve that the length of the tangents drawn from an external point to a circle are equal.
View SolutionProve that the length of the tangents drawn from an external point to a circle are equal.
View SolutionProve that the length of the tangents drawn from an external point to a circle are equal.
View SolutionProve that the length of the tangents drawn from an external point to a circle are equal.
View SolutionProve that the length of the tangents drawn from an external point to a circle are equal.
View SolutionProve that the length of the tangents drawn from an external point to a circle are equal.
View SolutionProve that the length of the tangents drawn from an external point to a circle are equal.
View Solution

