If P and Q are the mid points of the sides AB and CD of a parallelogram ABCD, prove that DP and BQ respectively.
Step by step video & image solution for If P\ a n d\ Q are the mid points of the sides AB and CD of a parallelogram ABCD, prove that DP and BQ respectively. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
If P and Q are the mid points of the sides AB and CD of a parallelogram ABCD, prove that DP and BQ cut the diagonal AC in its points of trisection which are also the points of trisection of DP and BQ respectively.
View SolutionE and F are the mid-points of the sides AB and CD of a parallelogram ABCD. Prove that the line segment AF and CE trisects BD in three equal parts.
View Solution
Knowledge Check
- Question 1 - Select One
If P and Q are the middle points of the sides BC and CD of the parallelogram ABCD, then AP+AQ is equal to
AACB12ACC23ACD32AC - Question 2 - Select One
X and Y are the mid-points of the opposite sides AB and DC of a parallelogram ABCD. Then □AXCY is a ?
ATrapeziumBKiteCRhombusDParallelogram - Question 3 - Select One or More
In the given figure, M is the mid-point of the side CD of the parallelogram ABCD. What is ON:OB?
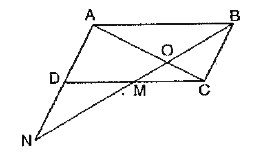 A3:2B2:1C3:1D5:2
A3:2B2:1C3:1D5:2
P and Q are the mid-point of the oposite sides AB and CD of a parallelogram ABCD. AQ interects DP at S and BQ interects CP at R. Show that PQRS is a parallelogram.
 View Solution
View SolutionThe middle points of the parallel sides AB and CD of a parallelogram ABCD are P and Q respectively. If AQ and CP divide the diagonal BD into three parts BX, XY and YD, then which one of the following is correct ?
View SolutionThe sides AB and CD of a parallelogram ABCD are bisected at EandF . Prove that EBFD is a parallelogram.
View SolutionABCD is a parallelogram. L and M are respectively mid points of sides AB and DC. Prove that LD and MB trisects diagonals AC.
View SolutionP, Q , R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
View Solution

