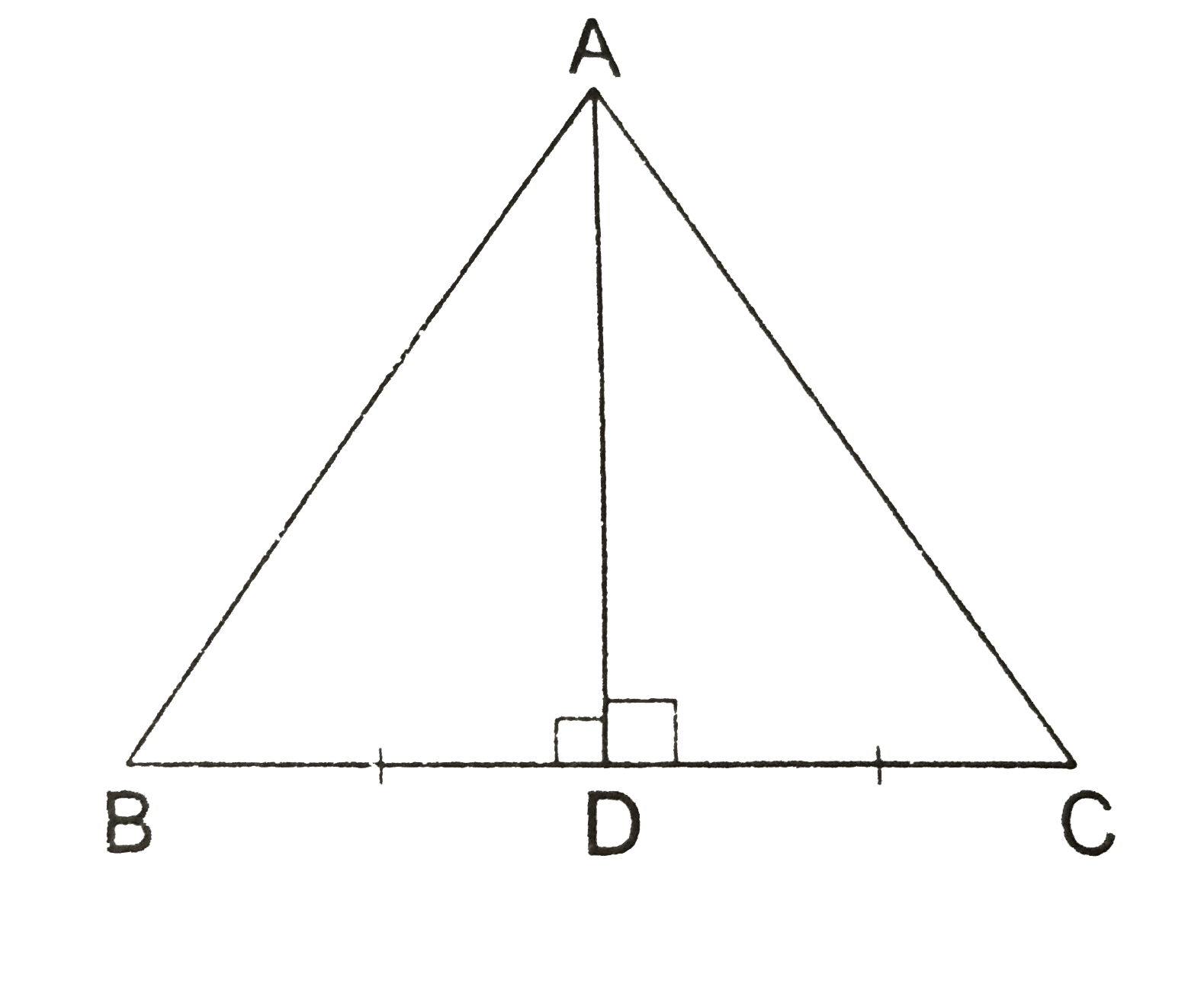
If the altitude from one vertex of a triangle bisects the opposite side; then the triangle is isosceless.
Given A ΔABC in which AD⊥BCandBD=DC.
TO PROVE AB = AC.
PROOF In ΔADBandΔADC, we have
BD = DC (given),
AD = AD (common)
and ∠ADB=∠ADC=90∘
∴ΔADB≅ΔADC (SAS-criteria).
Hence, Ab = AC (c.p.c.t.).
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9A
27 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9B
16 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)
37 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
22 Videos
Similar Questions
If the altitude from one vertex of a triangle bisects the opposite side, then the triangle is isosceles. GIVEN : A ABC such that the altitude AD from A on the opposite side BC bisects BC i.e., BD=DC. TO PROVE : AB=AC i.e. the triangle ABC is isosceles.
View SolutionWhich of the following statements are true (T) and which are false (F): Side opposite to equal angles of a triangle may be unequal. Angle opposite to equal sides of a triangle are equal. The measure of each angle of an equilateral triangle is 600. If the altitude from one vertex of a triangle bisects the opposite side, then the triangle may be isosceles. The bisectors of two equal angles of a triangle are equal. If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles. The two altitudes corresponding to two equal sides of a triangle need not be equal. If any two sides of a right triangle are respectively equal to two sides of other right triangle, then the two triangles are congruent. Two right triangles are congruent if hypotenuse and a side of one triangle are respectively equal to the hypotenuse and a side of the other triangle.
View Solution
Knowledge Check
If angle bisector of a triangle bisect the opposite side, then what type of triangle is it?
ARight angledBScaleneCSimilarDIsoscelesRead the statemenst carefully and state 'T' for true and 'F' for false .
1. If a line divides any two sides of a triangle in the same ratio , then the line is parallel to the third side of the triangle .
2 . The internal bisector of an angle of a triangle divides the opposite side inernally in the ratio of the sides containing the angle .
3 . If a line through one vertex of a triangle divides the opposite in the ratio of other two sides , then the line bisects the angle at the vertex .
4.Any line parallel to the parallel sides dividesproportionally .
5. Two times the sum of the squares of the sides of a triangle is equal to four times the sum of the squares of the medians of the triangle .A12345TTTTTB12345TTTTFC12345FTFTFD12345TTFTFIf the altitudes of a triangle are in AP, then the sides of the triangle are in
AAPBGPCHPDarithmetic-geometric progression
If the bisector of an angle of a triangle bisects the opposite side, prove that the triangle is isosceles.
View SolutionIf the altitudes from two vertices of a triangle to the opposite sides are equal, prove that the triangle is isosceles.
View SolutionIf the altitudes from two vertices of a triangle to the opposite sides are equal, prove that the triangle is isosceles.
In△ABEand △ACF∠AEB=∠AFC(900each)
∠BAE=∠CAF(common angle)
∠ABE=∠ACF using angle sum property
BE=CF,△ABE≅△ACF
⇒AB=AC
Hence triangle ABC is an isosceles tangent as two sides are equal to each other
View SolutionIf a line through one vertex of a triangle divides the opposite sides in the Ratio of other two sides; then the line bisects the angle at the vertex.
View SolutionIf the altitudes of a triangle are in A.P,then the sides of the triangle are in
View Solution
