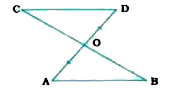
In the given figure, AB||CDandO is the midpoint of AD.
Show that (i) ΔAOB≅ΔDOC.
(ii) O is the midpoint of BC.

Step by step video & image solution for In the given figure, AB"||"CD and O is the midpoint of AD. Show that (i) DeltaAOB~=DeltaDOC. (ii) O is the midpoint of BC. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBook:RS AGGARWALChapter:CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEExercise:Exercise 9B
Explore 16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBook:RS AGGARWALChapter:CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEExercise:Multiple Choice Questions (Mcq)
Explore 20 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBook:RS AGGARWALChapter:CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEExercise:Multiple Choice Questions (Mcq)
Explore 20 Videos
- CIRCLES Book:RS AGGARWALChapter:CIRCLES Exercise:MULTIPLE CHOICE QUESTION(MCQ)
Explore 37 Videos
- COORDINATE GEOMETRYBook:RS AGGARWALChapter:COORDINATE GEOMETRYExercise:Multiple Choice Questions (Mcq)
Explore 22 Videos
Similar Questions
In the given figure. AB∣CDandO is the midpoint of AD.
View SolutionLine-segment AB is parallel to another line-segment CD. O is the mid-point of AD (see Fig. 7.15). Show that
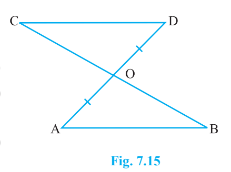
(i) ΔAOB≅ΔDOC
(ii) O is also the mid-point of BC
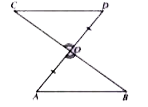
View SolutionIn the figure AB || CD, AD and BC intersect at o and O is mid-point of AD. Show that
(i) ΔAOB≅ΔDOCand(ii)OB=OC.
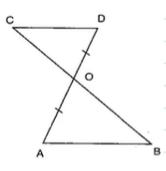
View SolutionIn Figure, line segment AB is parallel to another line segment CD . O is the mid-point of AD . Show that: (i)AOB≅DOC (ii)O is also the mid-point of BC.
View SolutionIn given figure, show that AB || CD
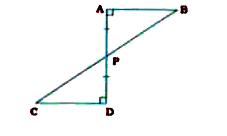
View SolutionIn the given figure, AB and DC are both perpendicular to line segment AD. BC intersects AD at P and P is the midpoint of AD. Prove that, ( 1 ) AB = CD ( 2 ) P is the midpoint of BC.
View SolutionLine segment AB is parallel to another line segment CD. O is the midpoint of AD (see the given figure). Show that
(i) △AOB=△DOC
(ii) O is also the midpoint of BC
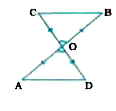
View SolutionIn the given figure, OA = OB and OD = OC. Show that
(i) ΔAOD≅ΔBOC and (ii) AD∣∣BC
View SolutionIn quadrilateral ABCD, AB||CD and BC||AD. Show that
(i) ΔABD≅ΔCDB

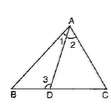
View SolutionIn Figure, if AD is the bisector of LA , show that: AB>BD (ii) AC>CD
View Solution