If the diagonals AC and BD intersect at point P in the cube in Figure what is the degree measure of angle APB ?

60
65
71
83
The correct Answer is:C
Look at the figure :
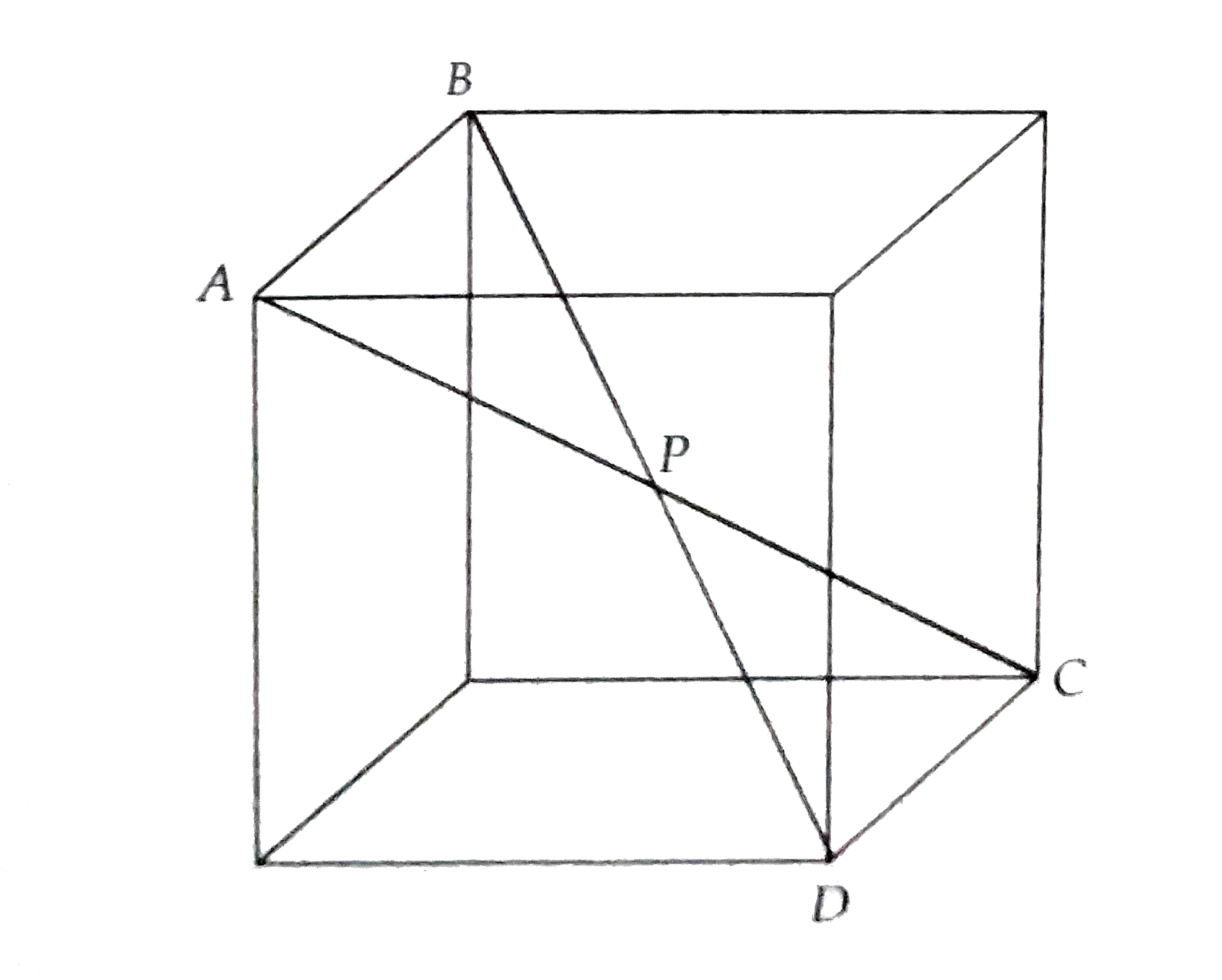
If we connect points A And D with a line segment and we connect points B and C with a line segment, then we will have a rectangle.

Side AB of rectangle ABCD is an edge of the cube. Since all edges of a cube have the same length, we can pick a number for the length of the edge of teh cube. Let's let the length of an edge of the cube be 1. So AB = 1. Diagonal AC of rectangle ABCD connects opposite vertices A and C of the cube. Now in any rectangular soild having a length l, a width w, and a height h, the formula for the distance d between opposite vertices is given by the formula . Here we have a cube, which is a rectangular solid where the length, width, and height are all equal. Since we are letting the edge of the cube be 1, we have that the length, width, and height are all equal to 1. So the length of AC is equal to .
We want the degree measure of angle APB. If we draw a perpendicular from point P to side AB of the rectangle and call the point where the perpendicular drawn from point P to side AB meets side AB point Q, then we will obtain two identical right triangles, triangles AQP and BQP.
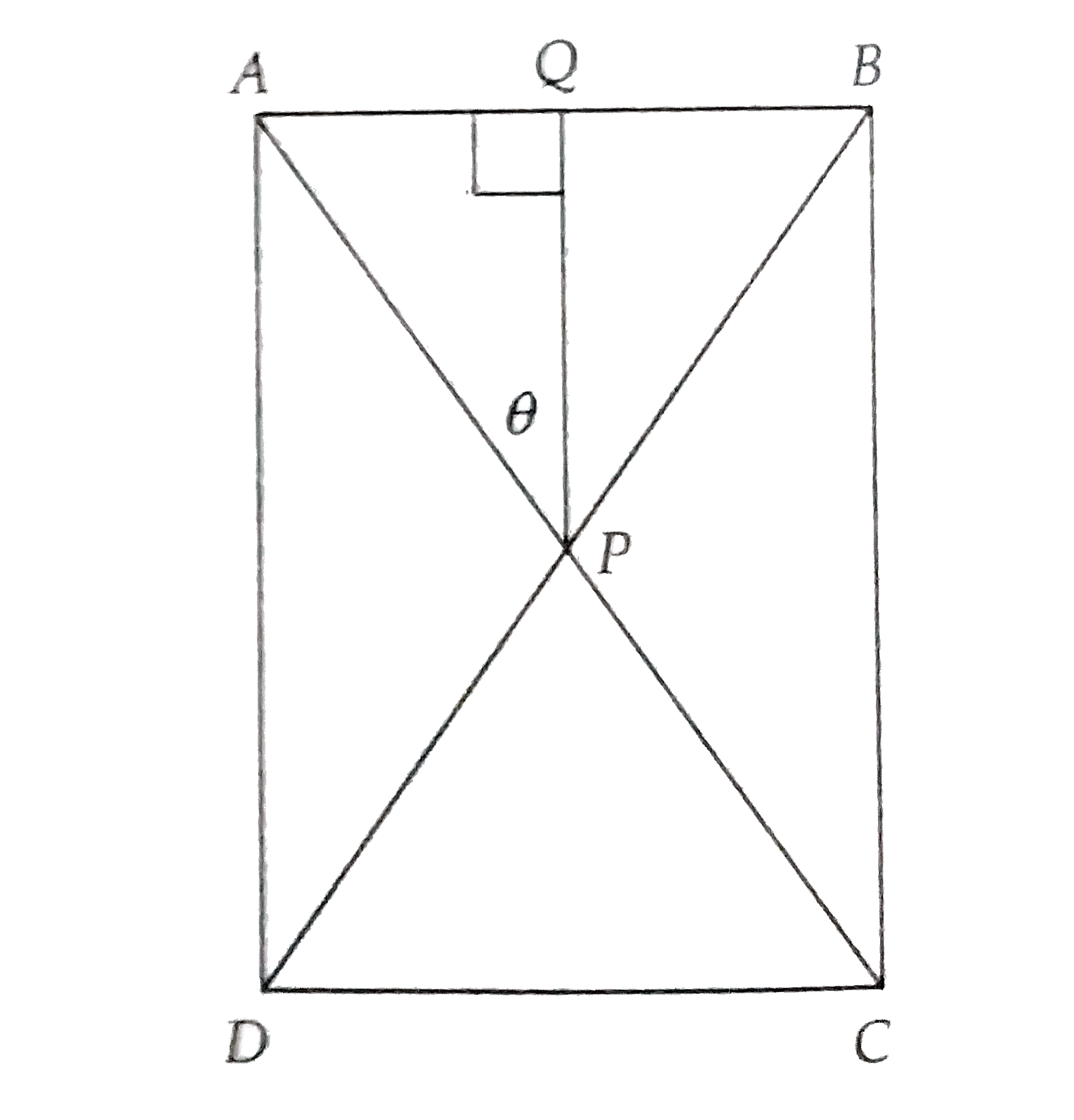
Point Q bisects AB. So the length of . Point P is the point of intersection of the diagonals, so point P is the midpoint of both diagonals. Therefore . Now angle APQ is of angle APB, whose degree measure we are seeking. Let's find the degree measure of angle APQ. Then we will take twice this number for the degree measure of angle APB. If we refer to angle APQ by the letter , then we have that sin
Thus, . So = arcsin . Use your calculator to find that and that = arcsin . So the degree measure of angle APB is approximately .
Topper's Solved these Questions
Similar Questions
In a rhombus ABCD the diagonals AC and BD intersect at the point (3,4) . If the point A is (1,2) the diagonal BD has the equation
View SolutionIn trapezium ABCD, side AB is parallel to side DC. Diagonals AC and BD intersect at point P. Prove that triangles APD and BPC are equal in area.
View Solution
Knowledge Check
- Question 1 - Select One
In this triangle, what is the degree measure of angle c ?
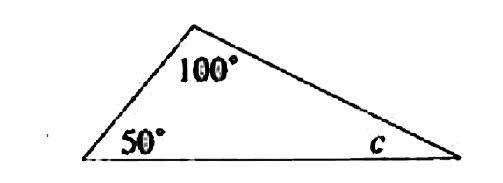 A17B20C30D40
A17B20C30D40 - Question 2 - Select One
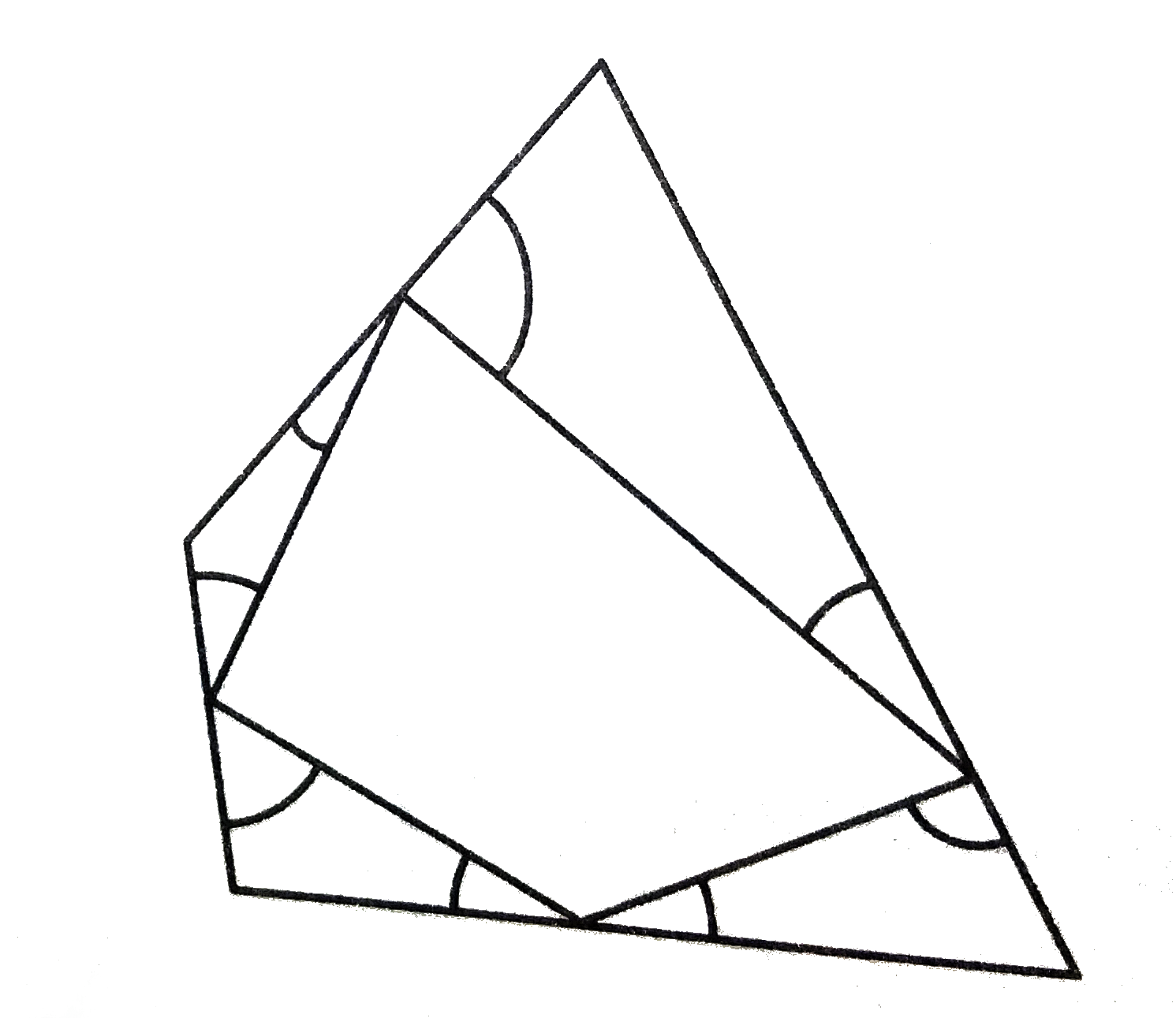
In the figure above, what is the sum of the degree measures of the marked angles?
A120B180C360DIt cannot be determined from the information given - Question 3 - Select One

In the figure above, what is the sum of the degree measures of all of the angles marked?A540B720C900D1080
In rhombus ABCD, diagonals AC and BD intersect each other at point O.
If cosine of angle CAB is 0.6 and OB = 8 cm, find the lengths of the side and the diagonals of the rhombus.View SolutionIf isosceles right triangle ABC and square ACDE share side AC, what is the degree measure of angle EBC ?
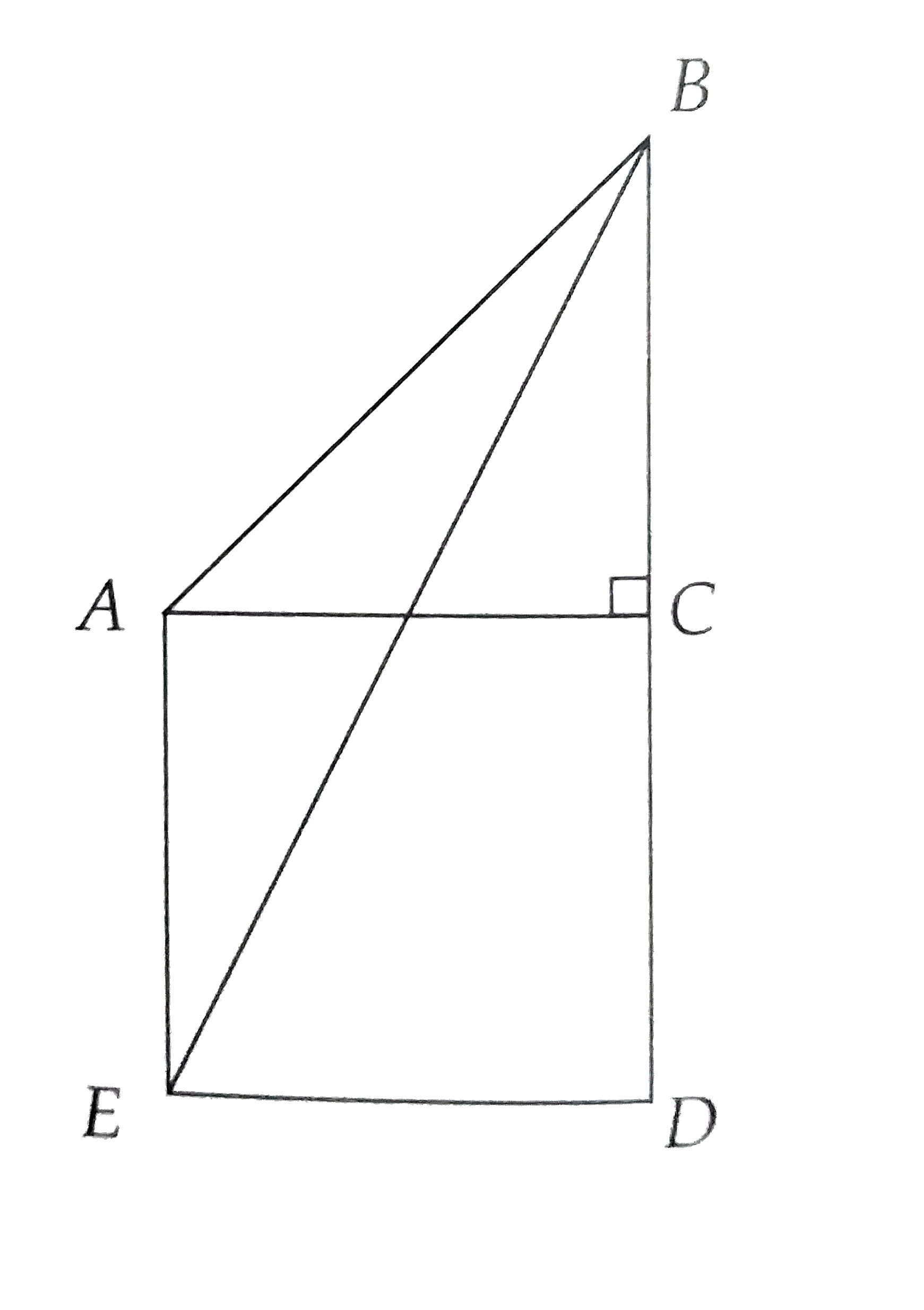 View Solution
View SolutionWhat is the degree measure, to the nearest integer, of angle ABO ?
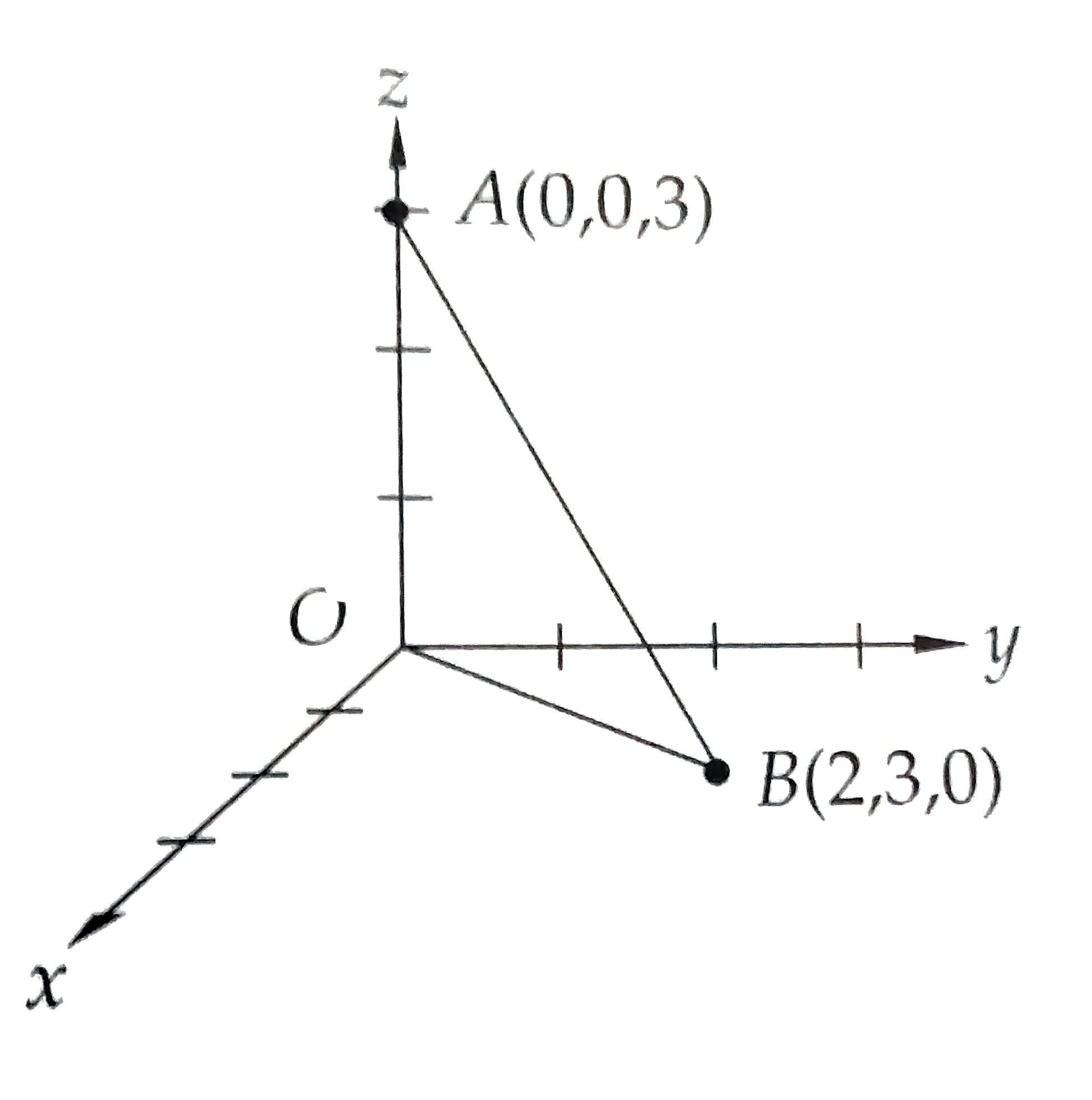 View Solution
View SolutionThe given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point P. If AP : CP = 3:5,

Find :
ΔADP:ΔAPBView SolutionABCD is a rhombus. Its diagonals ACandBD intersect at the point M and satisfy BD=2AC.If he point DandM represent the complex numbers 1+iand2−i respectively, then A represents the complex number......or......
View Solution

