If the feasibile region for a LPP is unbounded, maximum or minimum of the objective function Z = ax + by may or may not exist.
The correct Answer is:1
N/a
Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - FILLERS
7 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Fillers
18 Videos
- MATRICESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MATRICESEXERCISE - Solved example
101 Videos
Similar Questions
In the feasible region for a LPP is ..., then the optimal value of the objective function Z= ax + by may or may not exist.
View Solution
Z may not be:
View SolutionIn a LPP, the maximum value of the objective function Z = ax +by is always finite.
View SolutionIn a LPP, the objective function is always.
View SolutionFind the maximum and minimum values of the function f(x)=tanx−2x .
View SolutionThe feasible region for an LPP is shown in the following figure. Let F=3x−−4y be the objective function. Maximum value of F is
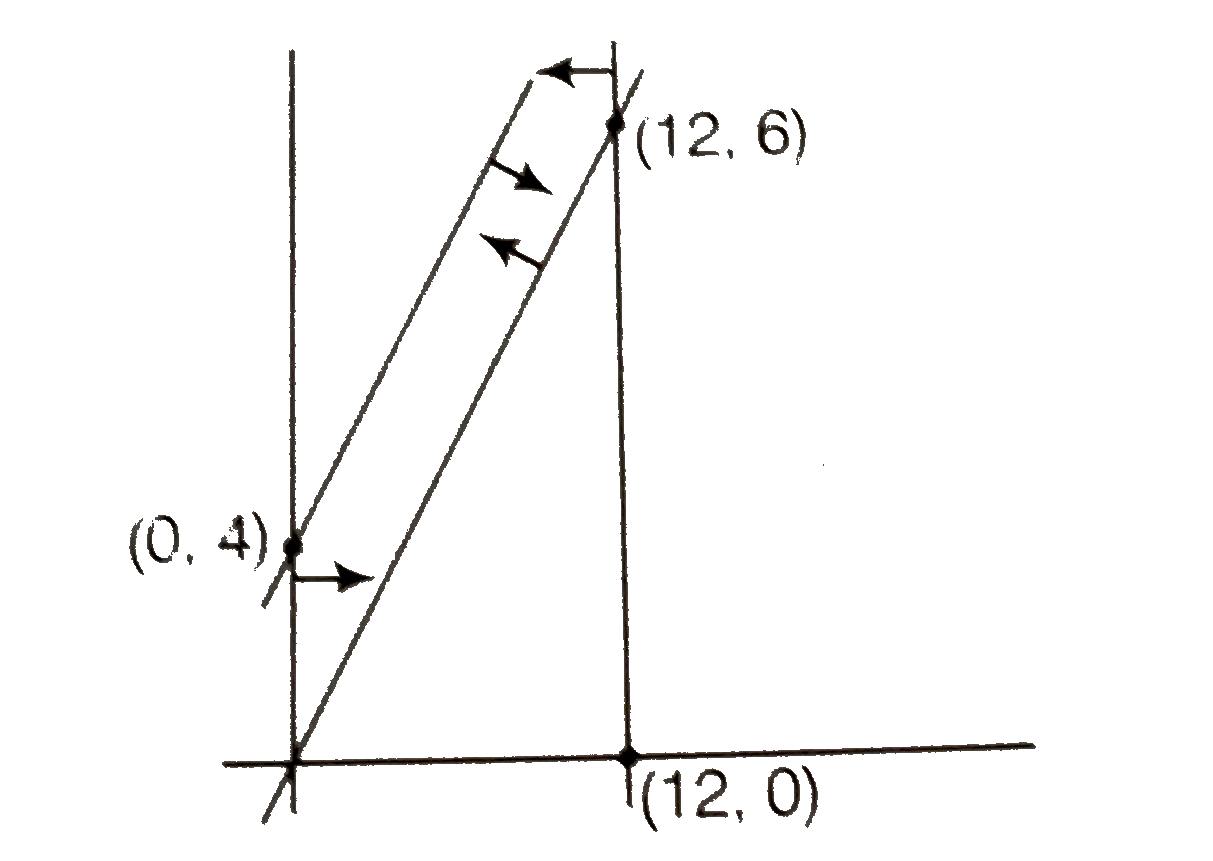
View SolutionThe feasible solution for a LPP is shown in following figure. Let Z=3x-4y be the objective function, Minimum of Z occurs at
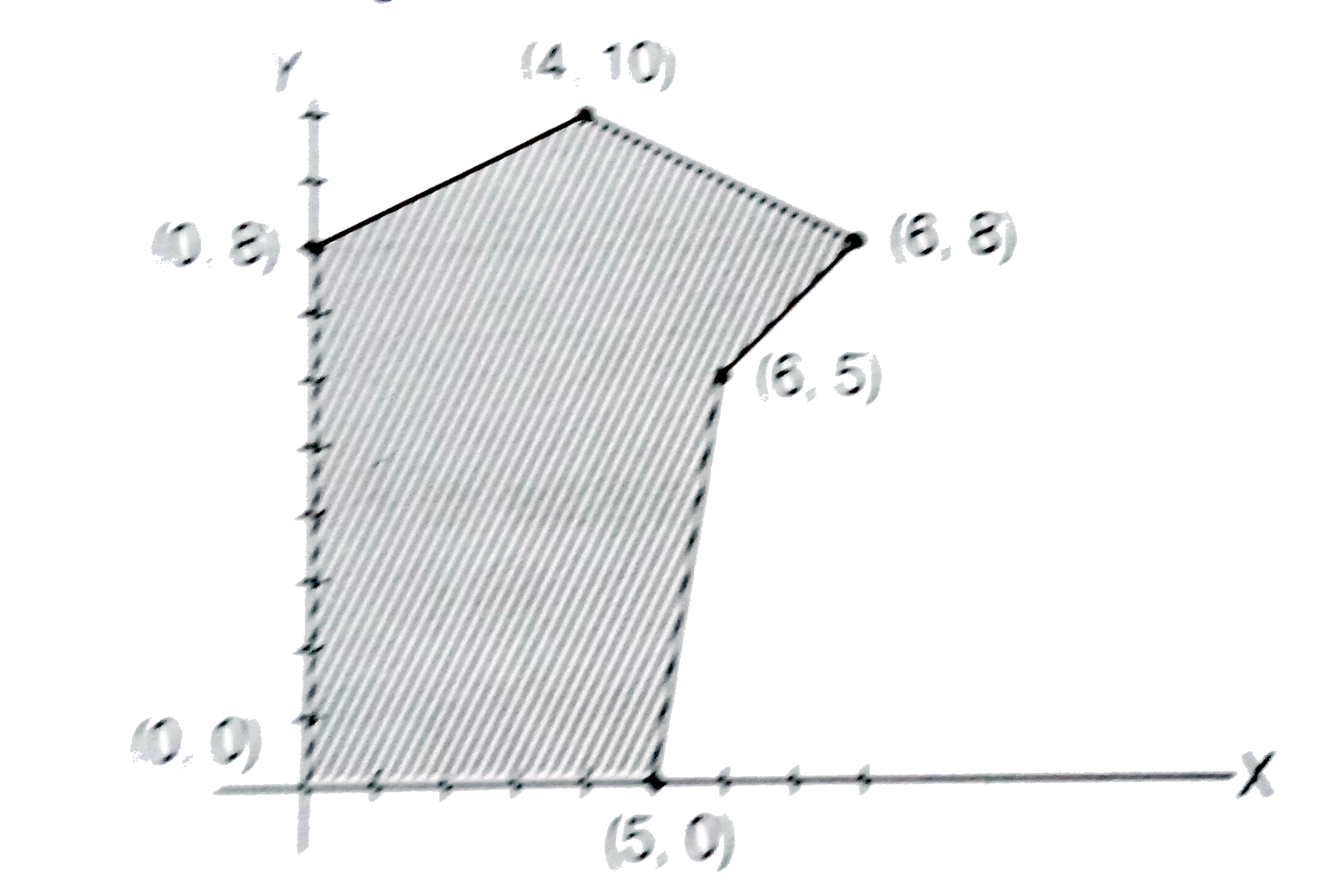
View SolutionIn the given graph,the feasible region for a LPP is shaded. The objective function Z=2x−3y,will be minimum at a) (4,10) b) (6,8) c) (0,8) d) (6,5)
View SolutionThe feasible region for an LPP is shown in following figure. Find the minimum value of Z=11x+7y.

View SolutionThe stem may function as :-
View Solution
