If the straight line x−2y+1=0 intersects the circle x2+y2=25 at points P and Q, then find the coordinates of the point of intersection of the tangents drawn at P and Q to the circle x2+y2=25.
Video Solution
Text Solution
Let R(h,k) be the point of intersection of the tangents drawn at P and Q to the given circle. Then PQ is the chord of the cord of tangents drawn from R to x2+y2=25
So, its equation is
hx+ky−25=0 (1)
It is given that the eqation of PQ is
x−2y+1=0 (2)
Since (1) and (2) represent the same line, we have
h1=k−2=−251
or h=−25,k=50
Hence, the required point is (−25,50)
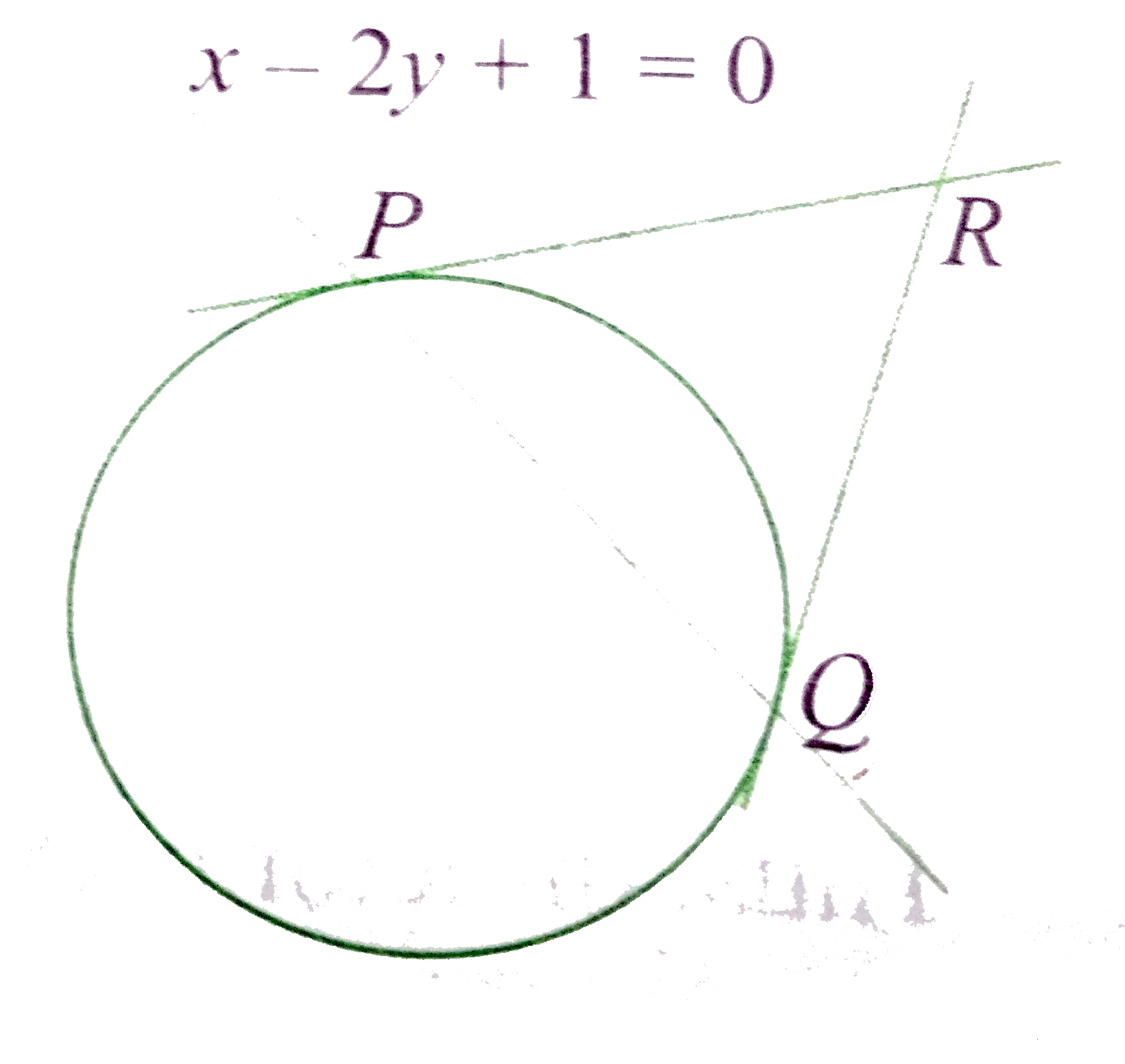
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The line 4x−7y+10=0 intersects the parabola y2=4x at the points P and Q. The coordinates of the point of intersection of the tangents drawn at the points P and Q are
A(−72,−52)B(52,72)C(−52,−72)D(72,52) - Question 2 - Select One
The straight lines y=±x intersect the parabola y2=8x in points P and Q, then length of PQ is
A4B4√2C8D16 - Question 3 - Select One
The straight lines y=±x intersect the parabola y2=8x in points P and Q, then length of PQ is
A4B4√2C8D16
if a variable tangent of the circle x2+y2=1 intersects the ellipse x2+2y2=4 at P and Q. then the locus of the points of intersection of the tangents at P and Q is
View SolutionThe lines joining the origin to the points of intersection of the line 4x+3y=24 with the circle (x−3)2+(y−4)2=25 are
View SolutionIf normal of circle x2+y2+6x+8y+9=0 intersect the parabola y2=4x at PandQ then find the locus of point of intersection of tangent's at PandQ.
View SolutionIf the circle x2+y2=a2 intersects the hyperbola xy = 25 in four points, then find the product of the ordinates of these points.
View SolutionLocus of point of intersection of perpendicular tangents to the circle x2+y2−4x−6y−1=0 is
View Solution

