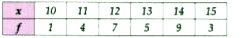If the sum of the mode and mean of a certain frequency distribution is 129 and the median of the observations is 63, mode and mean are respectively
69 and 60
65 and 64
68 and 61
none of these
The correct Answer is:A
To solve the problem step by step, we will use the information provided in the question about the mode, mean, and median of a frequency distribution.
Step 1: Set Up the Equations
We are given:
1. The sum of the mode (Mo) and mean (M) is 129.
Mo+M=129(Equation 1)
2. The median (Me) is given as 63.
Me=63
Step 2: Use the Relationship Between Mean, Median, and Mode
We can use the relationship between the mean, median, and mode:
3×Me=2×M+Mo
Substituting the value of the median:
3×63=2M+Mo
Calculating the left side:
189=2M+Mo(Equation 2)
Step 3: Solve the Equations Simultaneously
Now we have two equations:
1. Mo+M=129 (Equation 1)
2. 189=2M+Mo (Equation 2)
We can express Mo from Equation 1:
Mo=129−M
Now, substitute this expression for Mo into Equation 2:
189=2M+(129−M)
Simplifying this gives:
189=2M+129−M
189=M+129
Now, isolate M:
M=189−129
M=60
Step 4: Find the Mode
Now that we have the mean, we can find the mode using Equation 1:
Mo+60=129
Mo=129−60
Mo=69
Final Answer
Thus, the mode and mean are:
- Mode (Mo) = 69
- Mean (M) = 60
Summary
The mode and mean are respectively 69 and 60.
---
We are given:
1. The sum of the mode (Mo) and mean (M) is 129.
Mo+M=129(Equation 1)
2. The median (Me) is given as 63.
Me=63
We can use the relationship between the mean, median, and mode:
3×Me=2×M+Mo
Substituting the value of the median:
3×63=2M+Mo
Calculating the left side:
189=2M+Mo(Equation 2)
Now we have two equations:
1. Mo+M=129 (Equation 1)
2. 189=2M+Mo (Equation 2)
Mo=129−M
Now, substitute this expression for Mo into Equation 2:
189=2M+(129−M)
Simplifying this gives:
189=2M+129−M
189=M+129
Now, isolate M:
M=189−129
M=60
Now that we have the mean, we can find the mode using Equation 1:
Mo+60=129
Mo=129−60
Mo=69
Thus, the mode and mean are:
- Mode (Mo) = 69
- Mean (M) = 60
The mode and mean are respectively 69 and 60.
Topper's Solved these Questions
- MEASURES OF CENTRAL TENDENCYBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MEASURES OF CENTRAL TENDENCYEXERCISE - Exercise
40 Videos
- MAXIMA AND MINIMA BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MAXIMA AND MINIMA EXERCISE - Chapter Test
29 Videos
- MISCELLANEOUS EQUATIONS AND INEQUATIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MISCELLANEOUS EQUATIONS AND INEQUATIONS EXERCISE - Chapter Test
29 Videos
Similar Questions
Knowledge Check
If the median and mean of moderately asymmetrical frequency distribution are 72 and 74 respectively, then the mode is
A68B76C75D70
The mode for the following frequency distribution :

View SolutionFind the mode of the following frequency distribution :
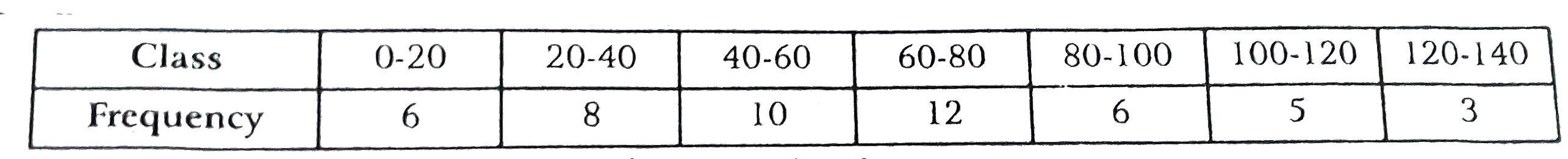
View SolutionFind the mean for the following frequency distribution :
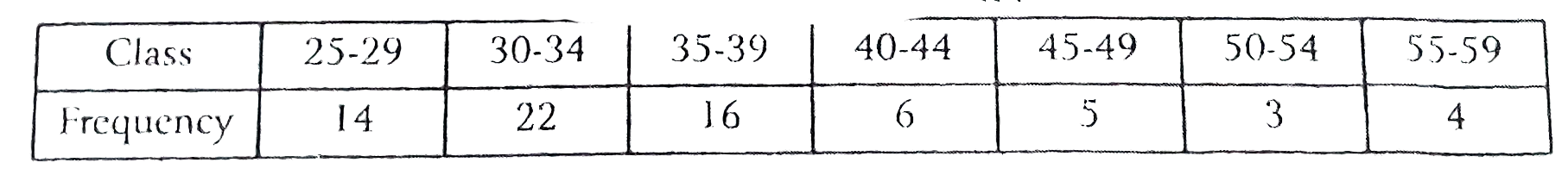
View SolutionCompute the mode for the following frequency distribution:
View SolutionCompute the mode for the following frequency distribution :

View SolutionCalculate the value of mode for the following frequency distribution :

View SolutionThe mean of the following frequency distribution is 57.6 and the sum of the observations is 50. Find the missing frquencies f1andf2 :

View Solution