If the velocity v of a particle moving along a straight line and its distance s from a fixed point on the line are related by , then its acceleration equals
as
s
2s
The correct Answer is:B
To solve the problem, we need to find the acceleration of a particle whose velocity v and distance s from a fixed point are related by the equation:
v2=a2+s2
1. Differentiate the Equation:
We start by differentiating both sides of the equation with respect to time t.
ddt(v2)=ddt(a2+s2)
2. Apply the Chain Rule:
Using the chain rule on the left side, we get:
2vdvdt=0+2sdsdt
Here, a2 is a constant, so its derivative is zero.
3. Simplify the Equation:
We can simplify the equation:
2vdvdt=2sdsdt
Dividing both sides by 2:
vdvdt=sdsdt
4. Recognize dsdt:
The term dsdt is the velocity v. Thus, we can rewrite the equation as:
vdvdt=sv
5. Isolate dvdt:
Now, we can divide both sides by v (assuming v≠0):
dvdt=s
6. Conclusion:
The acceleration a is defined as dvdt. Therefore, we have:
a=s
Final Answer:
The acceleration of the particle equals s.
We start by differentiating both sides of the equation with respect to time t.
Using the chain rule on the left side, we get:
We can simplify the equation:
The term dsdt is the velocity v. Thus, we can rewrite the equation as:
Now, we can divide both sides by v (assuming v≠0):
The acceleration a is defined as dvdt. Therefore, we have:
The acceleration of the particle equals s.
Topper's Solved these Questions
- DERIVATIVE AS A RATE MEASURER Book:OBJECTIVE RD SHARMA ENGLISHChapter:DERIVATIVE AS A RATE MEASURER Exercise:Section I - Solved Mcqs
Explore 27 Videos
- DEFINITE INTEGRALSBook:OBJECTIVE RD SHARMA ENGLISHChapter:DEFINITE INTEGRALSExercise:Chapter Test 2
Explore 56 Videos
- DIFFERENTIAL EQUATIONSBook:OBJECTIVE RD SHARMA ENGLISHChapter:DIFFERENTIAL EQUATIONSExercise:Chapter Test
Explore 30 Videos
Similar Questions
The speed v of a particle moving along a straight line. When it is at distance x from a fixed point on the line is v2=144−9x2. Select the correct alternatives
View SolutionThe speed v of a particle moving along a straight line. When it is at distance x from a fixed point on the line is v2=144−9x2. Select the correct alternatives
View SolutionThe speed (v) of particle moving along a straight line, when it is of a distance (x) from a fixed point on the line, is given by : v2=144−9x2
_S01_056_Q01.png)
View SolutionThe speed v of a particle moving along a straight line, when it is at a distance (x) from a fixed point of the line is given by v2=108−9x2 (all equation are in CGS units):
View SolutionIf the velocity v of particle moving along a straight line decreases linearly with its displacement s from 20ms−1 to a value approaching zero at s = 30 m, then acceleration of the particle at v=10ms^(-1) is
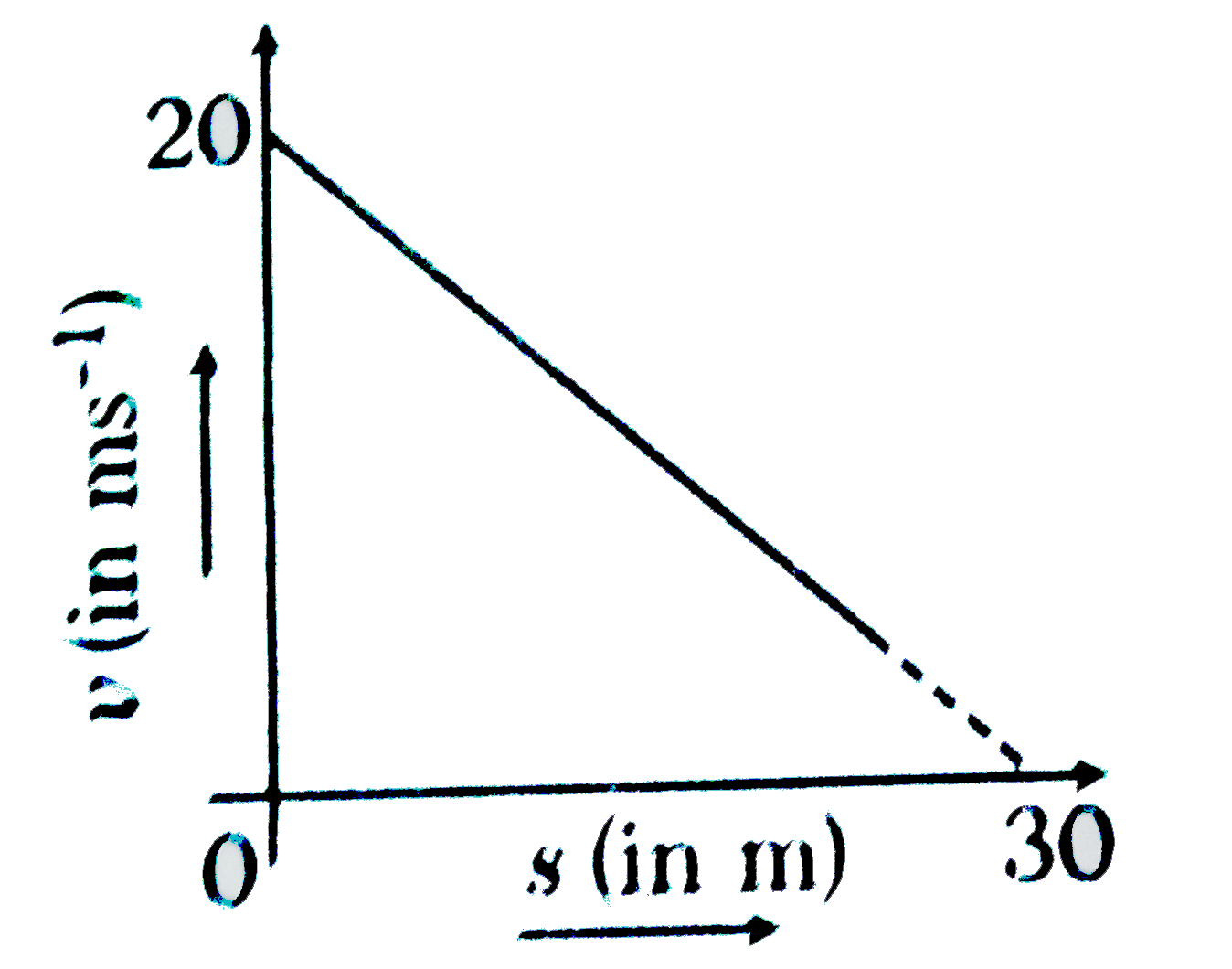
View SolutionIf the velocity v of a particle moving along a straight line decreases linearly with its displacement from 20m/s to a value approaching zero at s=30m, determine the acceleration of the particle when s=15m.
View SolutionThe distance covered by a particle moving in a straight line from a fixed point on the line is s, where s2=at2+2bt+c. Then prove that acceleration is proportional to s−3.
View SolutionA particle is moving along a straight line with increasing speed. Its angular momentum about a fixed point on this line :
View SolutionThe velocity –position graph of a particle moving along a straight line is shown. Then acceleration of the particle at s = 15 m is :

View SolutionThe distance covered by a particle moving in a straight line from a fixed point on the line is s, where s2=at2+2bt+⋅ Then prove that acceleration is proportional to s−3.
View Solution