If θ is the angle between the two radii (one to each circle) drawn from one of the point of intersection of two circles x2+y2=a2 and (x−c)2+y2=b2, then prove that the length of the common chord of the two circles is 2absinθ√a2+b2−2abcosθ
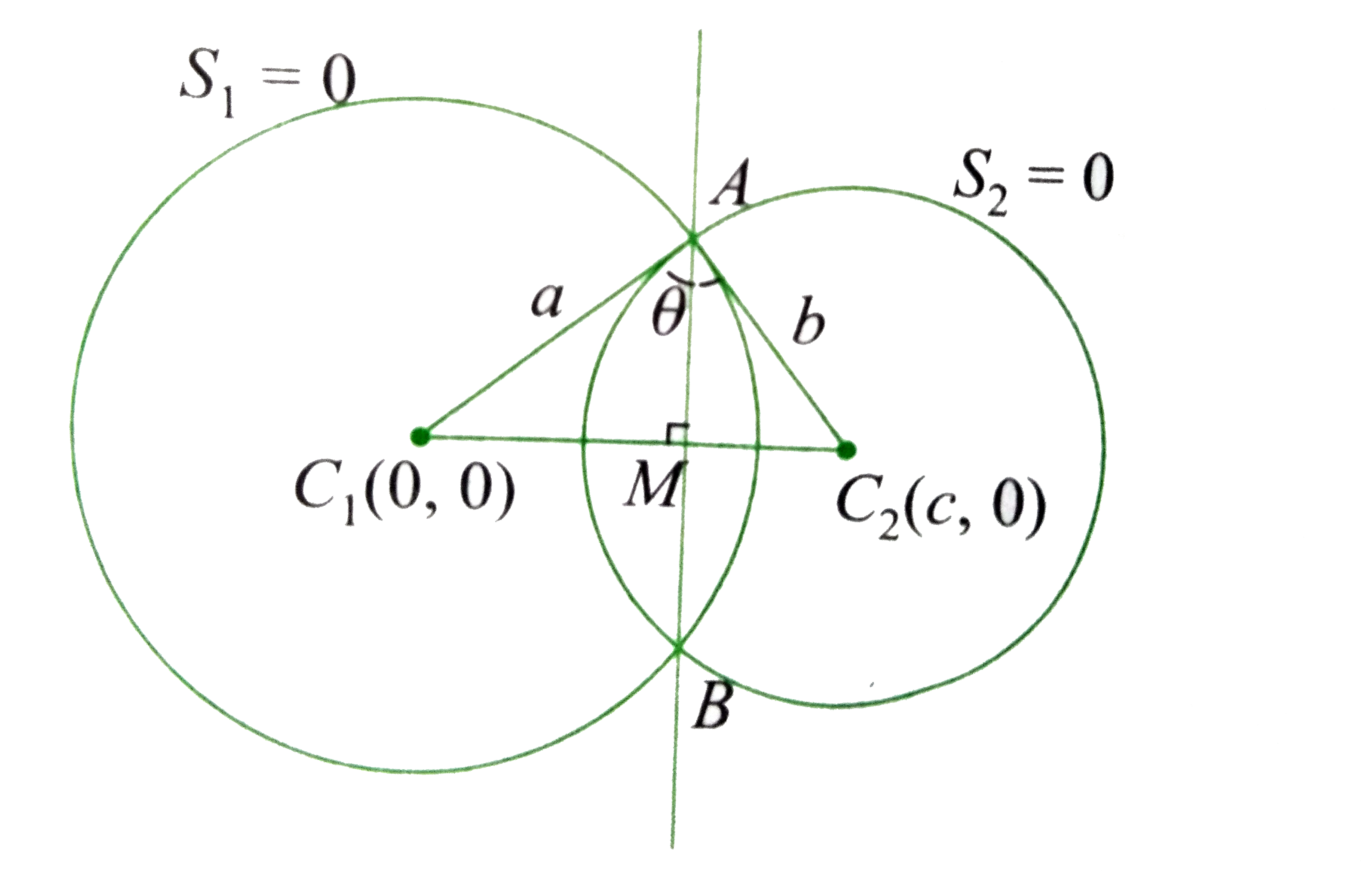
From the figure,
cosθ=a2+b2−c22ab
∴c=√a2+b2−2abcosθ=C1C2
Area of triangle C1AC2=12absinθ=12AM×C2C2
∴AM=absinθ√a2+b2−2abcosθ
∴ Length of common chord, AB=2AM=2absinθ√a2+b2−2abcosθ
Topper's Solved these Questions
Similar Questions
If θ is the angle between the two radii (one to each circle) drawn from one of the point of intersection of two circles x2+y2=a2 and (x−c)2+y2=b2, then prove that the length of the common chord of the two circles is 2absinθ√a2+b2−2abcosθ
View SolutionConsider the circle x2+y2=9andx2+y2−10x+9=0, then find the length of the common chord of circle is
View Solution
Knowledge Check
The angle of intersection of the two circles x2+y2−2x−2y=0andx2+y2=4 , is
A30∘B60∘C90∘D45∘The length of the common chord of the circles (x−a)2+(y−b)2=c2 and (x−b)2+(y−a)2=c2, is
A√c2−(a−b)2B√4c2−2(a−b)2C√2c2−(a−b)2D√4c2+(a−b)2The angle between the tangents drawn from a point on the director circle x2+y2=50 to the circle x2+y2=25, is
A45∘B60∘C90∘D120∘
If the circles x2+y2−2x−2y+7=0 and x2+y2+4x+2y+k=0 cut orthogonally, then the length of the common chord of the circles is a.12√13 b. 2 c. 5 d. 8
View SolutionIf the circles x2+y2+2gx+2fy+c=0 bisects x2+y2+2g'x+2f'y+c'=0 then the length of the common chord of these two circles is -
View SolutionThe length of the common chord of the circles (x−a)2+y2=r2 and x2+(y−b)2=r2 is
View SolutionIf the circle x2+y2+2gx+2fy+c=0 bisects the circumference of the circle x2+y2+2g'x+2f'y+c'=0, then the length of the common chord of these two circles is
View SolutionIf the circle x2+y2−2x−2y−1=0 bisects the circumference of the circle x2+y2=1 then the length of the common chord of the circles is
View Solution
