If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
Given Consider AB and CD are two equal chords of a circle, which meet at point E.
To prove AE=CE and BE=DE
Construction Draw OM⊥ABandON⊥CD and join OE where O is the centre of circle.
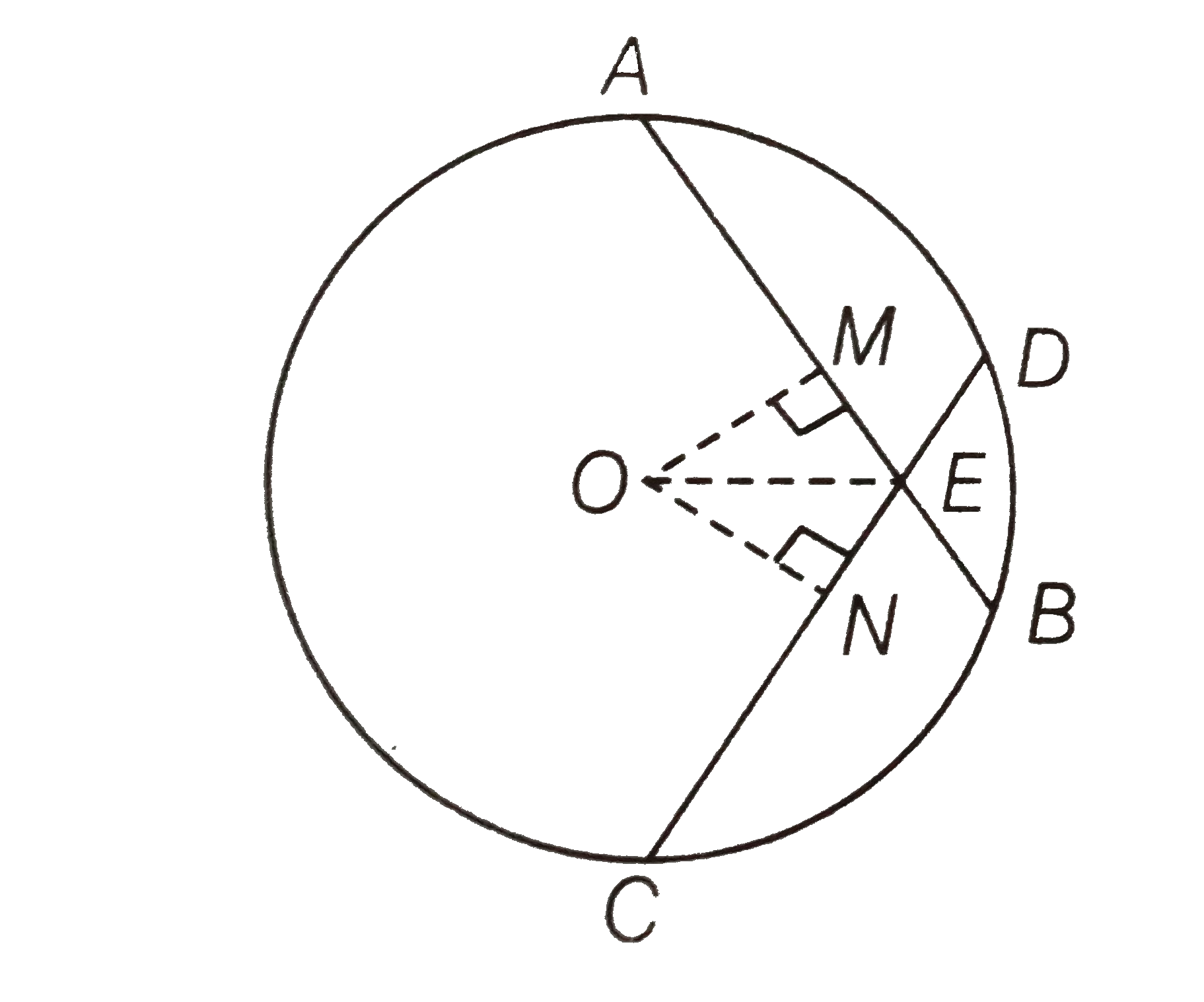
Proo In ΔOMEandΔONE,
OM=ON [equal chords are equidistant from the centre]
OE=OE [common side]
and ∠OME=∠ONE[each90∘]
∴ΔOME≅ΔONE [by RHS congurence rule]
⇒EM=EN [by CPCT]...(i)
Now, AB =CD
On dividing both sides by 2, we get
AB2=CD2⇒AM=CN ...(ii)
[ since, perpendicular drawn centre of circle to chord bisects the chord i.e., AM =MB and CN=ND]
On adding Eqs. (i) and (ii), we get
EM+AM=EN+CN
⇒AE+CE ....(iii)
Now, AB=CD
On subtracting both sides by AE, we get
AB-AE=CD-AE
⇒BE=CD−CE [form Eq. (iii)]
⇒BE=DE
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLARCHAPTER - CIRCLESEXERCISE - Exercise 10.4
2 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLARCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Areas Of Parallelograms And Triangles
34 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLARCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
If two equal chords of a circle in intersect within the circle, prove that: the segments of the chord are equal to the corresponding segments of the other chord. the line joining the point of intersection to the centre makes equal angles with the chords.
View SolutionIf two equal chords of a circle in intersect within the circle, prove that : the segments of the chord are equal to the corresponding segments of the other chord. the line joining the point of intersection to the centre makes equal angles with the chords.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the center makes equal angles with the chords.
View SolutionEqual chords of a circle are equidistant from circle.
View SolutionEqual chords of a circle are equidistant from the centre.
View SolutionIf two chords of a circle intersect inside or outside the circle when produced ; the rectangle formed by the two segments of one chord is equal in area to the rectangle formed by the two segments of the other chord.
View SolutionTheorem of internal division of chords.
Suppose two chords of a circle intersect each other in the interior of the circle, then the product of the lengths of the two segments of one chord is equal to the product of the lengths of the two segments of the other chord.
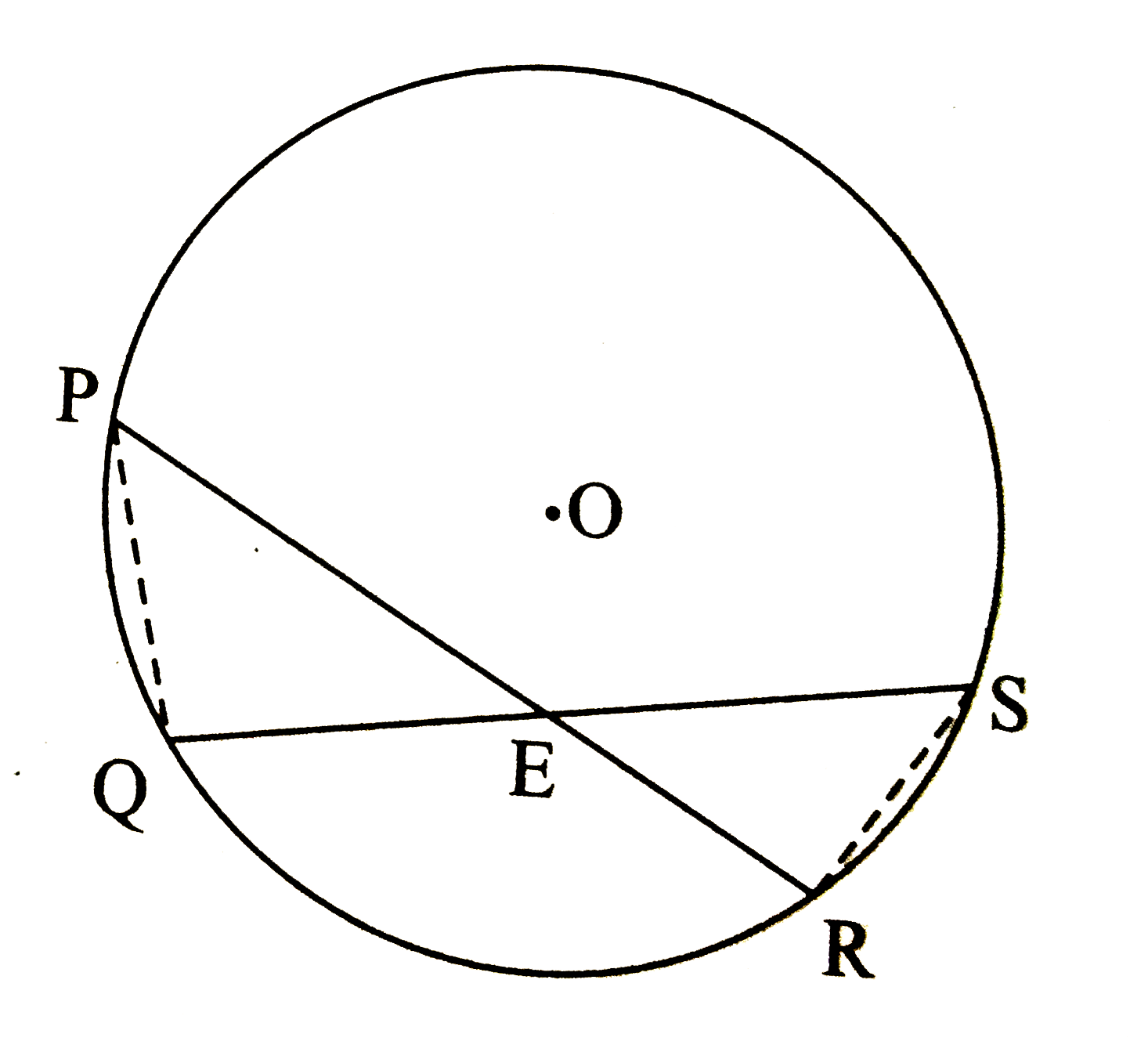
Given : (1) A circle with centre O .
(2) chords PR and QS intersect at point E inside the circle.
To prove : PE × ER = QE xx ES <br>Construction: Draw seg PQ and seg RS
View SolutionA chord of a circle of radius 12 cm subtends an angle of 120∘ at the centre . Find the area of the corresponding segment of the circle.
View SolutionEqual chords of a circle subtend equal angles at the centre.
View SolutionIf the two equal chords of a circle intersect :
(i) inside
(ii) on
(iii) outside
the circle, then show that the line segment joining the point of intersection to the centre of the circle will bisect the angle between the chords.
View Solution
