If two interior angles on the same side of a transversal intersecting two parallel lines are in the ratio 2:3, then the measure of the larger angle is
36∘
72∘
108∘
54∘
The correct Answer is:C
To solve the problem, we will follow these steps:
Step 1: Understand the problem
We have two interior angles on the same side of a transversal intersecting two parallel lines, and these angles are in the ratio of 2:3. We need to find the measure of the larger angle.
Step 2: Define the angles
Let the two angles be represented as:
- Angle 1 = 2x
- Angle 2 = 3x
Step 3: Use the property of interior angles
Since these angles are on the same side of the transversal, their sum is equal to 180 degrees:
Angle 1+Angle 2=180∘
Substituting the expressions for the angles:
2x+3x=180∘
Step 4: Combine like terms
Combine the terms on the left:
5x=180∘
Step 5: Solve for x
To find the value of x, divide both sides by 5:
x=180∘5
Calculating this gives:
x=36∘
Step 6: Find the measures of the angles
Now, substitute x back into the expressions for the angles:
- Angle 1 = 2x = 2(36) = 72 degrees
- Angle 2 = 3x = 3(36) = 108 degrees
Step 7: Identify the larger angle
The larger angle is:
Angle 2=108∘
Conclusion
Thus, the measure of the larger angle is 108 degrees.
---
We have two interior angles on the same side of a transversal intersecting two parallel lines, and these angles are in the ratio of 2:3. We need to find the measure of the larger angle.
Let the two angles be represented as:
- Angle 1 = 2x
- Angle 2 = 3x
Since these angles are on the same side of the transversal, their sum is equal to 180 degrees:
Angle 1+Angle 2=180∘
Substituting the expressions for the angles:
2x+3x=180∘
Combine the terms on the left:
5x=180∘
To find the value of x, divide both sides by 5:
x=180∘5
Calculating this gives:
x=36∘
Now, substitute x back into the expressions for the angles:
- Angle 1 = 2x = 2(36) = 72 degrees
- Angle 2 = 3x = 3(36) = 108 degrees
The larger angle is:
Angle 2=108∘
Thus, the measure of the larger angle is 108 degrees.
Topper's Solved these Questions
Similar Questions
If the angle of a triangle are in the ratio 2:1:3, then find the measure of smallest angle.
View SolutionAlternate interior angles between parallel lines are equal
View SolutionTheorem 6.4 : If a transversal intersects two parallel lines, then each pair of interior angles on the same side of the transversal is supplementary.
View SolutionTheorem 6.2 : If a transversal intersects two parallel lines, then each pair of alternate interior angles is equal.
View SolutionTwo supplementary angles are in the ratio 2:3. Find the angles.
View SolutionTwo supplementary angles are in the ratio 2:3. Find the angles.
View SolutionIf two acute angles of a right angled triangle are in the ratio 2 : 3 , find the measure of all angles of the triangle.
View SolutionTwo complementary angles are in the ratio 2:3, find these angles
View SolutionRead the following statements which are taken as axioms
(i) If a transversal intersects two parallel lines, then corresponding angles are not necessarily equal.
(ii) If a transversal intersect two parallel lines, then alternate interior angles are equal.
Is this system of axioms consistent ? Justify your answer.View SolutionAP and BQ are the bisectors of the two alternate interior angles formed by the intersection of a transversal t with parallel lines l and m (in the given figure). Show that AP||BQ.
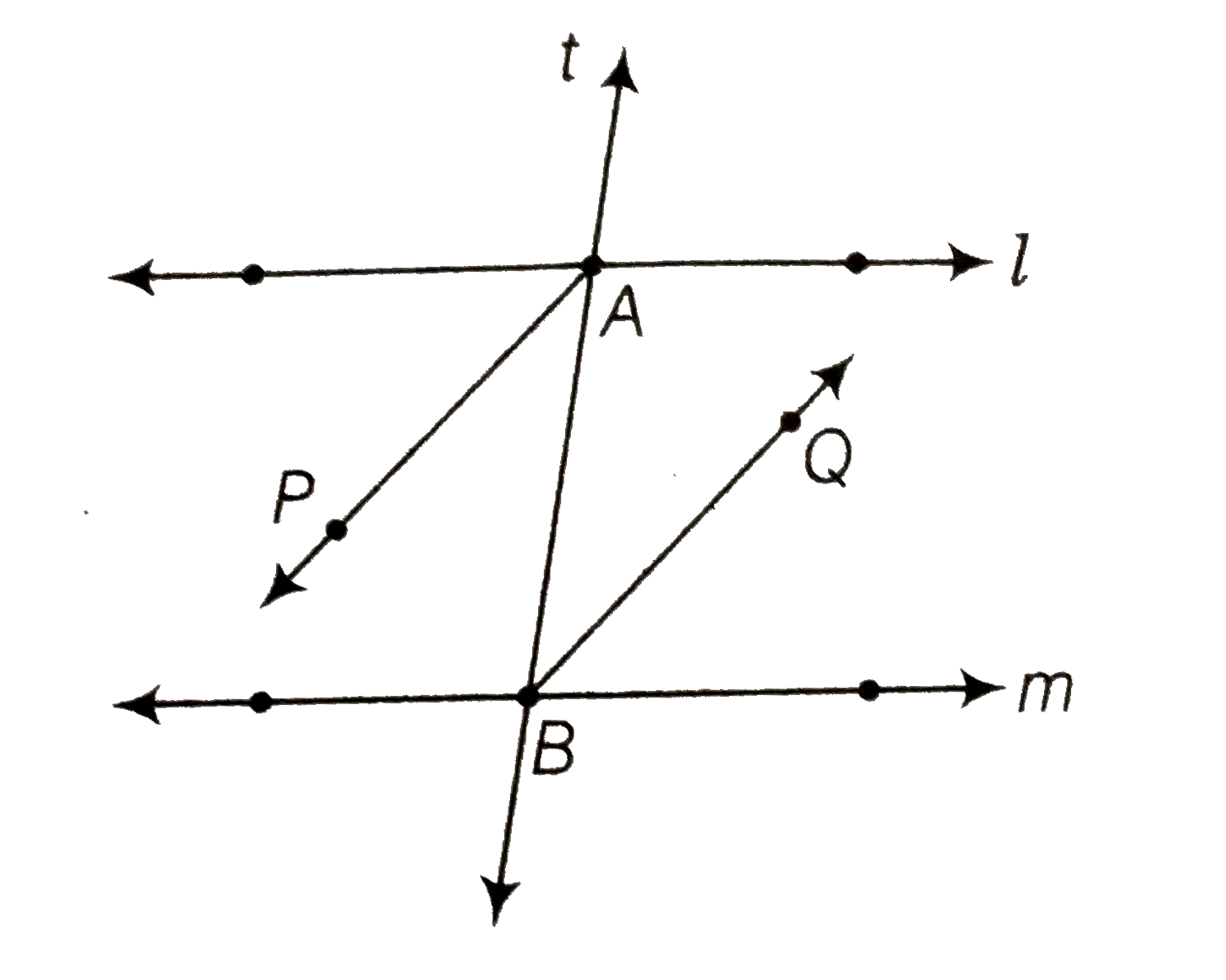 View Solution
View Solution

