AP and BQ are the bisectors of the two alternate interior angles formed by the intersection of a transversal t with parallel lines l and m (in the given figure). Show that AP||BQ.
Given In the figure l||m , AP and BQ are the bisectors of ∠EAB and ∠ABH, respectively.
To Prove AP|| BQ
Proof Since, l||m and t is transversal.
Therefore, ∠EAB=∠ABH [alternate interior angles]
⇒ 12∠EAB=12∠ABH [dividing both sides by 2]
⇒ ∠PAB=∠ABQ [AP and BQ are the bisectors of ∠EABand∠ABH]
Since, ∠PAB and ∠ABQ are alternate interior angles with two lines AP and BQ and transversal AB, Hence, AP || BQ.
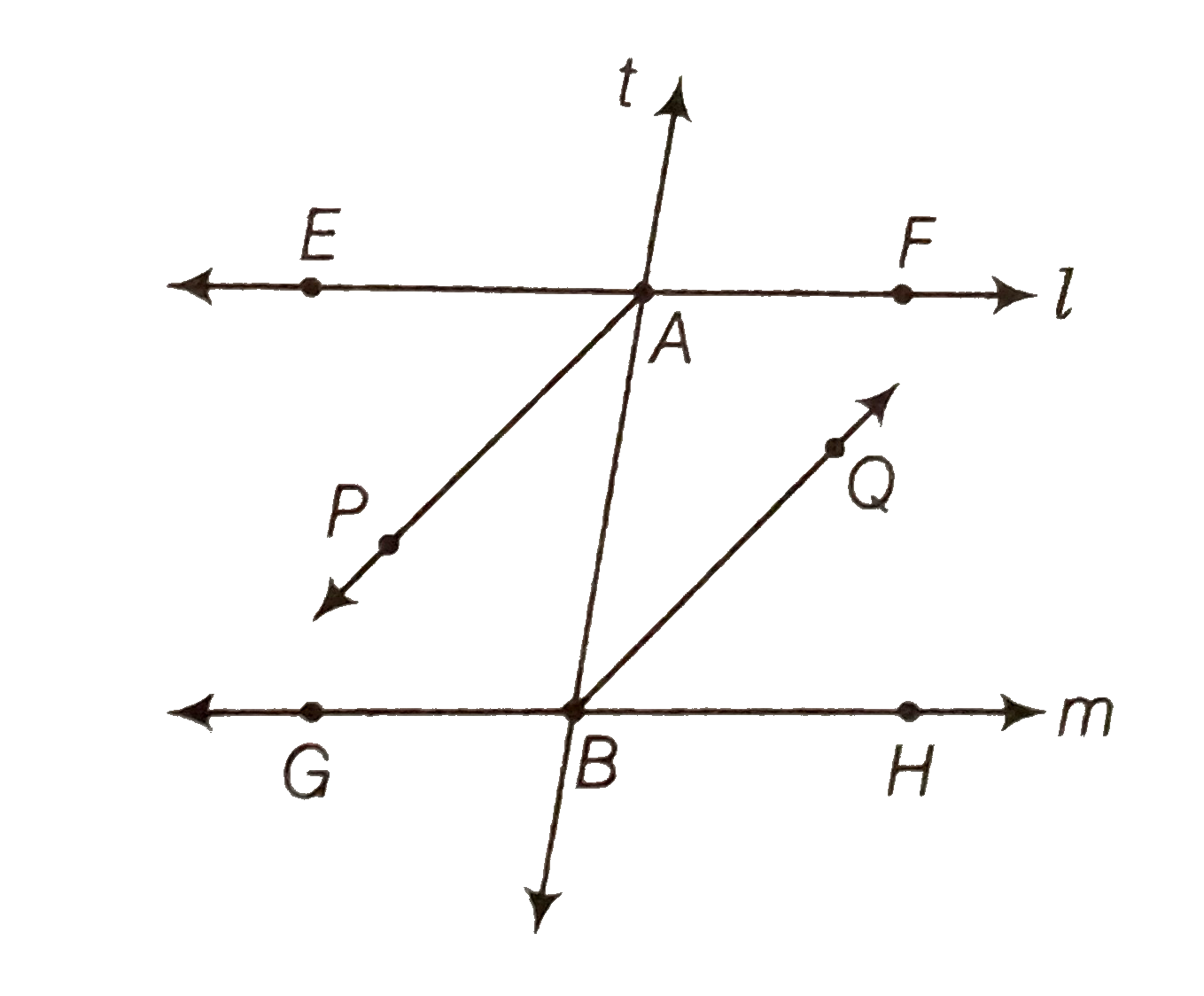
Topper's Solved these Questions
Similar Questions
If the bisectors of a pair of alternate angles formed by a transversal with two given lines are parallel, prove that the given lines are parallel.
View SolutionIn the given figure, bisectors AP and BQ of the alternate interior angles are parallel, then show that l ||m.
View SolutionIf the bisectors of a pair of corresponding angles formed by a transversal with two given lines are parallel;prove that the given lines are parallel.
View Solutionl and m are two parallel lines intersected by another pair of parallel lines p and q as shown in figure. Show that ABC≅CDA
View SolutionIn the adjoining figure, transversal n cuts parallel lines l and m. If ∠5=65∘, find all other angles

View Solutionl and m are two parallel lines intersected by another pair of parallel lines p and q as shown in figure. Show that △ABC≅△CDA.
View SolutionIf one of the four angles formed by two intersecting lines is a right angle, then show that each of the four angles is a right angle.
View SolutionRead the following statements which are taken as axioms
(i) If a transversal intersects two parallel lines, then corresponding angles are not necessarily equal.
(ii) If a transversal intersect two parallel lines, then alternate interior angles are equal.
Is this system of axioms consistent ? Justify your answer.
View SolutionIf two parallel lines are intersected by a transversal, prove that the bisectors of the interior angles on the same side of transversal intersect each other at right angles.
View SolutionIn the given figure, a transversal n cuts two lines l and m if ∠1=700 and ∠7=800, is l ∣∣ m?
View Solution
