Question

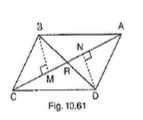
In a $ABC,BMandCN$
are perpendiculars from
$BandC$
respectively on any
line passing through $A\stackrel{.}{}$
If $L$
is the mid-point of $BC$
, prove that $ML=NL$.

Explanation

Construction: Draw `OL` perpendicular to `MN`.
Now, If a transversal makes equal intercepts on three or more parallel lines, then any other transversal intersecting them will also make equal intercepts.
`BM`, `CN` and `OL` are perpendicular to `MN`
Therefore, `BM` parallel to `CN` parallel to `OL`.
Now, `BM` parallel to `CN` parallel to `OL` and `BC` is the transversal making equal intercepts
i.e. `BL=LC`
Therefore, transversal `MN` willl also make equal intercepts.
`OM=ON`
In triangles `LMO` and `LNO`,
`OM=ON`
`angleLOM=angleLON=90^@`
`OL` is common
As both triangles are congruent.
`therefore LM =LN (CPCT)`
Hence Proved.