In a circel with centre O. chords AB and CD interest inside the circumference at E. Prove that ∠AOC+BOD=2∠AEC.
Consider arc AC of the circle with centre at O.
Clearly, arc AC subtends ∠AOC at the centre and ∠ABC at the remaining part of the circle.
∴∠AOC=2∠ABC ...........(1)
Similarly,arc BD subtends ∠BOD at the centre and ∠BCD at the remaining part of the circle.
∠BOD=2∠BCD .........(2)
Adding eqs.(1) and (2) , we get
∠AOC+∠BOD=2(∠ABC+∠BCD)
⇒∠AOC+∠BOD=2∠AEC
(∵∠AEC is the exterior angle and ∠ABC and ∠BCD are other interior angles of ΔBEC∴∠ABC+∠BCD=∠AEC)

Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10a
22 Videos
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10b
19 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
Knowledge Check
In a circle with centre O, chords AB and CD intersect inside the circumference at E. Find ∠AEC. If ∠AOC=40∘and∠BOD=50∘.
A90∘B45∘C30∘D60∘AB is a diameter of the circle with centre O and chord CD is equal to radius OC (fig). AC and BD proudced meet at P. Prove that ∠CPD=60∘.
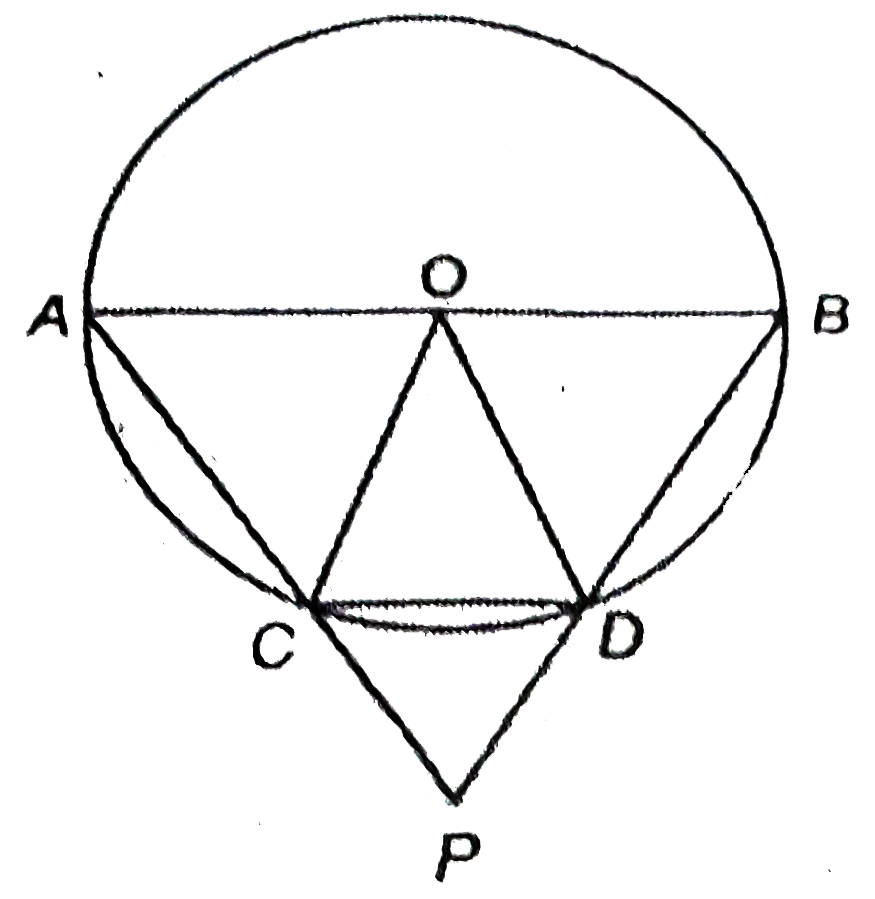 A60∘B30∘C90∘D160∘
A60∘B30∘C90∘D160∘In a circle with the centre is O and AB is the diameter of the circle and CD is the chord of the circle. If angle ABC is 54∘ and the length of CD and BC is equal, then find the ∠DBC.
A1. 36∘B2. 24∘C3. 48∘D4. 12∘
In a circle with centre O, chords AB and CD intersect inside the circumference at E. Prove that ∠AOC+ ∠BOD=2 ∠AEC
View SolutionIf AB is chord of a circle with centre O, AOC is a diameter and AT is the tangent at A as shown in figure. Prove that ∠BAT=∠ACB.
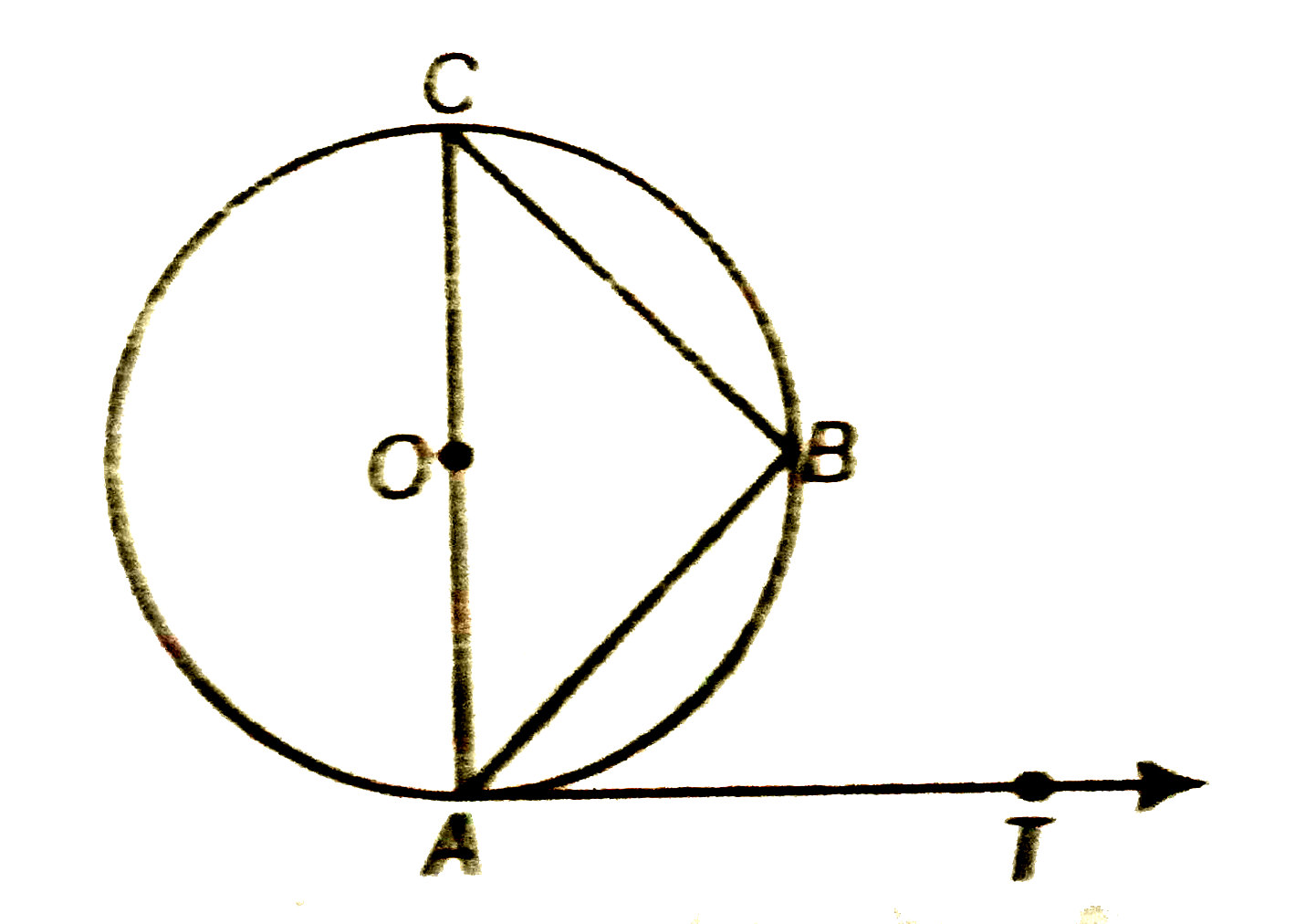
View SolutionIn a circle , O is the centre of the circle. Chords AB and CD intersect at P. If ∠AOD=32∘ and ∠COB=26∘, then the measure of ∠APD lies between:
केंद्र O के साथ एक वृत्त में, जीवा AB और CD,P पर प्रतिच्छेद करते हैं, यदि ∠AOD=32∘ और ∠COB=26∘ तो ∠APD का माप किसके बीच में होगा
View SolutionIf O is the circumference of a △ABC and OD perpendicular BC, prove that angle BOD = angle A.
View SolutionIf two chords AB and AC of a circle with centre O are such that the centre O lies on the bisector of ∠BAC; Prove that AB=AC
View Solution
