In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in Fig. 12.24. Find the area of the design (shaded region).

We use the concept of areas of circle and equilateral triangle in the problem.
Mark O as center of the circle. Join BO and CO.
Since we know that equal chords of a circle subtend equal angles at the center and all sides of an equilateral triangle are equal,
Each side of △ABC will subtend equal angles at the center.
∠BOC=360∘3=120∘
Consider △BOC. Drop a perpendicular from OM to BC
We know perpendicular from the center of circle to a chord bisects it.
BM=MC
OB=OC (radii)
OM=OM (common)
△OBM≅△OCM (by SSS congruency)
∠BOM=∠COM (by CPCT)
2∠BOM=∠BOC=120∘
∠BOM=120∘2=60∘
sin60∘=BMBO=√32
BM=√32×BO=√32×32=16√3
BC=2BM=32√3
Using the formula of area of equilateral triangle = √34(side)2
We can find the area of △ABC since a side BC of △ABC is known.
Visually from the figure, it’s clear that
Area of the design = Area of circle - Area of △ABC = πr2−√34(BC)2
This can be solved with ease as both the radius of the circle and BC are known.
Radius of circle (r) = 32cm
From figure, we observe area of design = Area of circle - Area of △ABC
= πr2−√34(BC)2
= 227×(32)2−√34×(32√3)2
= 227×1024−√34×1024×3
= 225287−768√3
Area of design = (225287−768√3)cm²
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - EXERCISE 12.15videos
AREAS RELATED TO CIRCLES
- BOOK - NCERTCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - SOLVED EXAMPLES6videos
AREAS RELATED TO CIRCLES
- BOOK - NCERTCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - SOLVED EXAMPLES6videos
AREAS RELATED TO CIRCLES
- BOOK - NCERTCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - Exercise 5.320videos
ARITHMETIC PROGRESSIONS
Similar Questions
In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in Fig. 12.24. Find the area of the design (shaded region).
 View Solution
View SolutionIn a circulat table cover of radius 42 cm, a design is formed, leaving an equilateral triangle ABC in the middle as shown in the figure.
Find the area of the design. [ Use √3=1.73]
 View Solution
View SolutionIn a circular table cover of radius 32 cm, a design (shade) is formed leaving an equilateral traingle ABC in the middle as shown in the adjacent figure.Find the area of the shaded region.
View SolutionIn a circular table cover of radius 32cm, a design is formed leaving an equilateral triangle ABC as shown in figure. Find the area of shaded region.
View SolutionIn the given Fig. 12.30, find the area of the shaded region.
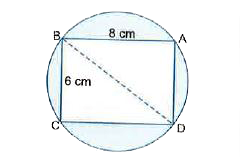 View Solution
View SolutionConsider an equilateral triangle of side √6 as shown in figure. Find the area of the shaded region
View SolutionA girl formed of design in a circle of radius 42 cm leaving an equilateral triangle ABC in the middle as shown in the figure. Find the corvered area of the design. (Use √3=1.73andπ=227)
 View Solution
View SolutionFind the area of the shaded region shown in the fig.
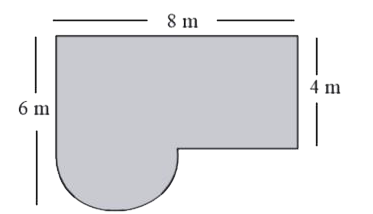 View Solution
View SolutionABC is an equilateral triangle inscribed in a circle of radius 4 cm. Find the area of the shaded portion.
 View Solution
View SolutionIn the adjoining figure, PQR is an equilateral triangle inscribed in a circle of radius 7cm. Find the area of the shaded region.
View Solution

