In a ΔABC,∠B is an acute-angle and AD⊥BC
Prove that :
(i) AC2=AB2+BC2−2BC×BD
(ii) AB2+CD2=AC2+BD2
To prove the statements given in the question, we will use the Pythagorean theorem and some algebraic manipulations. Let's go through the proofs step by step.
Given:
- Triangle ABC with angle B as an acute angle.
- AD is perpendicular to BC, where D is the foot of the perpendicular from A to BC.
To Prove:
1. AC2=AB2+BC2−2⋅BC⋅BD (i)
2. AB2+CD2=AC2+BD2 (ii)
Proof:
Part (i):
1. Consider Triangle ADB:
- Since AD is perpendicular to BC, triangle ADB is a right triangle.
- By the Pythagorean theorem, we have:
AB2=AD2+BD2(1)
2. Consider Triangle ADC:
- Triangle ADC is also a right triangle.
- By the Pythagorean theorem, we have:
AC2=AD2+CD2(2)
3. Express CD in terms of BC and BD:
- Since D lies on BC, we can express CD as:
CD=BC−BD
4. Substituting CD in equation (2):
- Substitute CD into equation (2):
AC2=AD2+(BC−BD)2
- Expanding (BC−BD)2:
(BC−BD)2=BC2−2⋅BC⋅BD+BD2
- Therefore, we have:
AC2=AD2+BC2−2⋅BC⋅BD+BD2
5. Using equation (1):
- From equation (1), we know AD2=AB2−BD2.
- Substitute AD2 into the equation:
AC2=(AB2−BD2)+BC2−2⋅BC⋅BD+BD2
- Simplifying gives:
AC2=AB2+BC2−2⋅BC⋅BD
- Thus, we have proved part (i).
Part (ii):
1. Using equations (1) and (2):
- From equation (1):
AB2=AD2+BD2
- From equation (2):
AC2=AD2+CD2
2. Rearranging equation (2):
- Rearranging gives:
AB2−AC2=AD2+BD2−(AD2+CD2)
- This simplifies to:
AB2−AC2=BD2−CD2
3. Rearranging to prove the required statement:
- Rearranging gives:
AB2+CD2=AC2+BD2
- Thus, we have proved part (ii).
Conclusion:
We have successfully proved both statements:
1. AC2=AB2+BC2−2⋅BC⋅BD
2. AB2+CD2=AC2+BD2
- Triangle ABC with angle B as an acute angle.
- AD is perpendicular to BC, where D is the foot of the perpendicular from A to BC.
1. AC2=AB2+BC2−2⋅BC⋅BD (i)
2. AB2+CD2=AC2+BD2 (ii)
1. Consider Triangle ADB:
- Since AD is perpendicular to BC, triangle ADB is a right triangle.
- By the Pythagorean theorem, we have:
AB2=AD2+BD2(1)
- Triangle ADC is also a right triangle.
- By the Pythagorean theorem, we have:
AC2=AD2+CD2(2)
- Since D lies on BC, we can express CD as:
CD=BC−BD
- Substitute CD into equation (2):
AC2=AD2+(BC−BD)2
- Expanding (BC−BD)2:
(BC−BD)2=BC2−2⋅BC⋅BD+BD2
- Therefore, we have:
AC2=AD2+BC2−2⋅BC⋅BD+BD2
- From equation (1), we know AD2=AB2−BD2.
- Substitute AD2 into the equation:
AC2=(AB2−BD2)+BC2−2⋅BC⋅BD+BD2
- Simplifying gives:
AC2=AB2+BC2−2⋅BC⋅BD
- Thus, we have proved part (i).
1. Using equations (1) and (2):
- From equation (1):
AB2=AD2+BD2
- From equation (2):
AC2=AD2+CD2
- Rearranging gives:
AB2−AC2=AD2+BD2−(AD2+CD2)
- This simplifies to:
AB2−AC2=BD2−CD2
- Rearranging gives:
AB2+CD2=AC2+BD2
- Thus, we have proved part (ii).
We have successfully proved both statements:
1. AC2=AB2+BC2−2⋅BC⋅BD
2. AB2+CD2=AC2+BD2
Similar Questions
In a ΔABC, ∠B is an acute-angle and AD⊥BC. Prove that:
AB2+CD2=AC2+BD2View SolutionIn fig. ∠B of △ABC is an acute angle and AD⊥BC ; prove that AC2=AB2+BC2−2BC×BD
View SolutionIn figure, ∠B<90∘andAD⊥BC. Prove that AC2=AB2+BC2−2BC.BD
View SolutionIn the figure , ABC is triangle in which ∠ABC<90∘andAD⊥BC. Prove that AC2=AB2+BC2−2BC⋅BD.
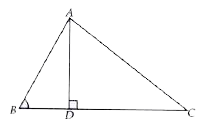 View Solution
View Solution(Result on acute triangle) In Fig. 4.184, ∠B of ABC is an acute angle and AD⊥BC , prove that AC2=AB2+BC2−2 BC×BD
View SolutionIn the given figure if AD ⊥ BC prove that AB2+CD2=BD2+AC2
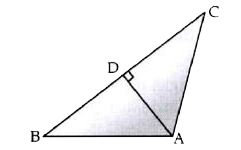 View Solution
View SolutionIn aΔABC,AD is a median and AL⊥BC.
Prove that
(a) AC2=AD2+BC⋅DL+(BC2)2
(b) AB2=AD2−BC⋅DL+(BC2)2
(c) AC2+AB2=2AD2=2AD2+12BC2
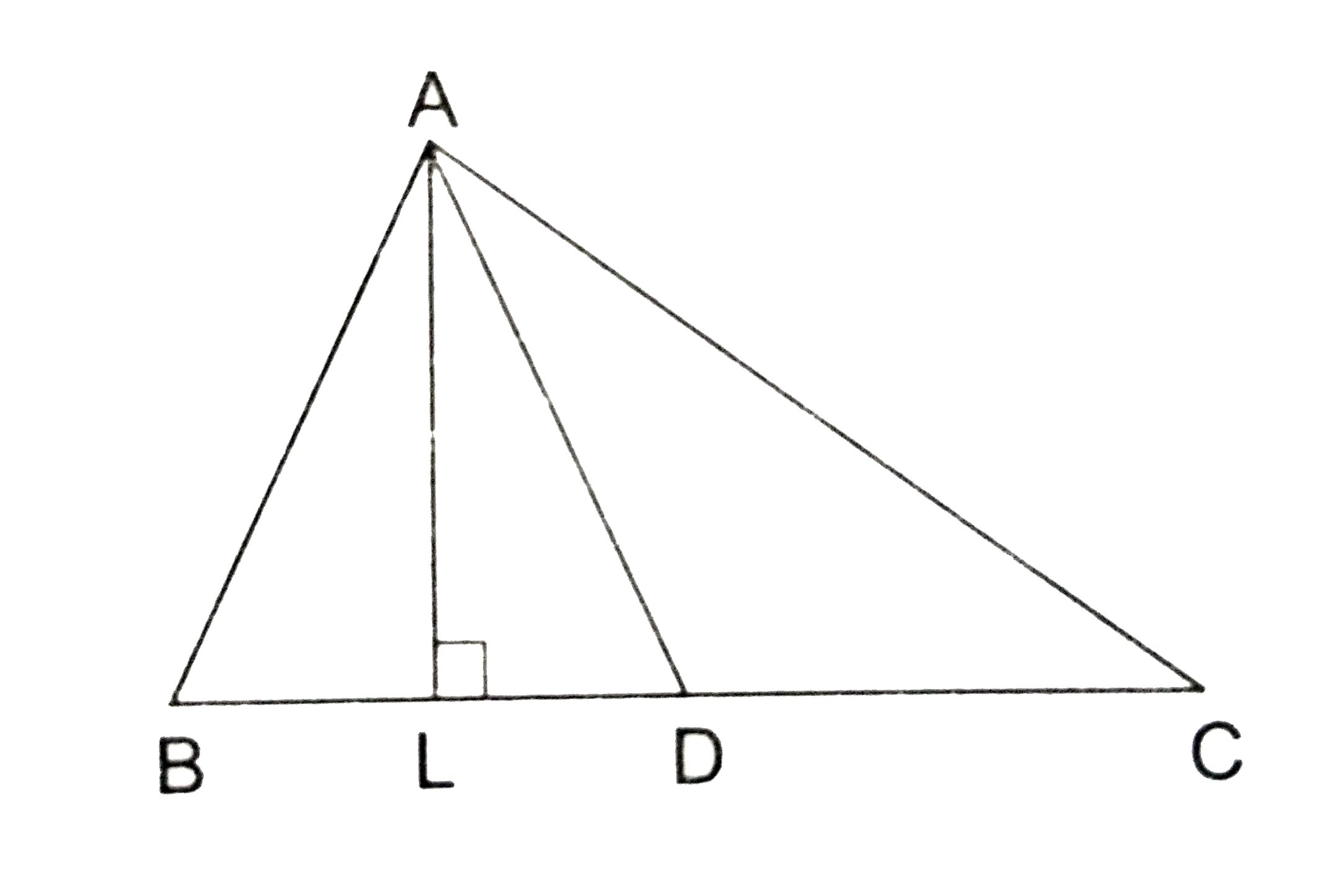 View Solution
View SolutionIn ΔABC,∠A=90∘,AB=AC,D is any point on BC. Provew that BD2+CD2=2AD2.
View SolutionIn ΔABC, seg AD⊥ seg BCDB=3CD.
Prove that : 2AB2=2AC2+BC2
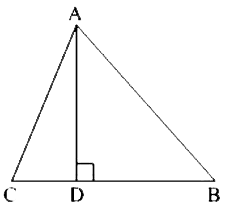 View Solution
View SolutionIn ABC , AD is perpendicular to BC . Prove that: AB2+CD2=AC2+BD2 (ii) AB2−BD2=AC2−CD2
View Solution

