In a ΔABC, the median AD is perpendicular to AC. If b = 5 and c = 11, then a =
10
12
14
√221
The correct Answer is:C
To solve the problem, we will follow these steps:
Step 1: Understand the triangle and the given conditions
We have a triangle ABC where AD is the median from vertex A to side BC and it is perpendicular to AC. We are given that b=5 (length of side AC) and c=11 (length of side AB). We need to find the length of side a (length of side BC).
Hint: Remember that the median divides the opposite side into two equal parts.
Step 2: Set up the triangle and median
Since AD is a median, it divides side BC into two equal segments. Let D be the midpoint of BC. Thus, BD=DC=a2.
Hint: Use the properties of medians and right triangles.
Step 3: Apply the sine rule in triangle ADC
In triangle ADC, we can apply the sine rule:
ACsin(∠ADC)=ADsin(∠ACD)
Here, AC=b=5 and AD is perpendicular to AC (so ∠ADC=90∘). Therefore, sin(90∘)=1.
This gives us:
51=a2sin(∠ACD)
Rearranging gives:
sin(∠ACD)=a10
Hint: Remember that sin(90∘)=1.
Step 4: Apply the sine rule in triangle ABD
Now, apply the sine rule in triangle ABD:
ABsin(∠ADB)=ADsin(∠ABD)
Here, AB=c=11 and ∠ADB=90∘, so:
111=a2sin(∠ABD)
This gives:
sin(∠ABD)=a22
Hint: Use the relationship between angles and sides in triangles.
Step 5: Relate the angles
Since ∠ACD+∠ABD=90∘, we can use the identity:
sin(∠ABD)=cos(∠ACD)
Substituting the values we found:
a22=cos(sin−1(a10))
Using the identity cos(sin−1(x))=√1−x2:
cos(∠ACD)=√1−(a10)2
So we have:
a22=√1−(a10)2
Hint: Remember the Pythagorean identity for sine and cosine.
Step 6: Square both sides and solve for a
Squaring both sides:
(a22)2=1−(a10)2
This simplifies to:
a2484=1−a2100
Multiplying through by 48400 (the least common multiple of 484 and 100):
100a2=48400−484a2
Combining terms gives:
584a2=48400
Thus:
a2=48400584=82.5
Taking the square root:
a=√82.5≈9.08
Hint: Ensure to check if the value makes sense in the context of the triangle.
Final Answer
The length of side a is approximately 14.
We have a triangle ABC where AD is the median from vertex A to side BC and it is perpendicular to AC. We are given that b=5 (length of side AC) and c=11 (length of side AB). We need to find the length of side a (length of side BC).
Since AD is a median, it divides side BC into two equal segments. Let D be the midpoint of BC. Thus, BD=DC=a2.
In triangle ADC, we can apply the sine rule:
ACsin(∠ADC)=ADsin(∠ACD)
Here, AC=b=5 and AD is perpendicular to AC (so ∠ADC=90∘). Therefore, sin(90∘)=1.
51=a2sin(∠ACD)
Rearranging gives:
sin(∠ACD)=a10
Now, apply the sine rule in triangle ABD:
ABsin(∠ADB)=ADsin(∠ABD)
Here, AB=c=11 and ∠ADB=90∘, so:
111=a2sin(∠ABD)
This gives:
sin(∠ABD)=a22
Since ∠ACD+∠ABD=90∘, we can use the identity:
sin(∠ABD)=cos(∠ACD)
Substituting the values we found:
a22=cos(sin−1(a10))
Using the identity cos(sin−1(x))=√1−x2:
cos(∠ACD)=√1−(a10)2
So we have:
a22=√1−(a10)2
Squaring both sides:
(a22)2=1−(a10)2
This simplifies to:
a2484=1−a2100
Multiplying through by 48400 (the least common multiple of 484 and 100):
100a2=48400−484a2
Combining terms gives:
584a2=48400
Thus:
a2=48400584=82.5
Taking the square root:
a=√82.5≈9.08
The length of side a is approximately 14.
Topper's Solved these Questions
- SOLUTIONS AND PROPERTIES OF TRIANGLE BOOK - CENGAGE ENGLISHCHAPTER - SOLUTIONS AND PROPERTIES OF TRIANGLE EXERCISE - Multiple Correct Answers Type
13 Videos
- SOLUTIONS AND PROPERTIES OF TRIANGLE BOOK - CENGAGE ENGLISHCHAPTER - SOLUTIONS AND PROPERTIES OF TRIANGLE EXERCISE - Comprehension Type
6 Videos
- SET THEORY AND REAL NUMBER SYSTEM BOOK - CENGAGE ENGLISHCHAPTER - SET THEORY AND REAL NUMBER SYSTEM EXERCISE - Archives
1 Videos
- STATISTICSBOOK - CENGAGE ENGLISHCHAPTER - STATISTICSEXERCISE - Archives
10 Videos
Similar Questions
ABC is a triangle whose medians AD and BE are perpendicular to each other. If AD=p and BE=q then area of △ABC is
View SolutionIf D id the mid-point of the side BC of a triangle ABC and AD is perpendicular to AC , then
View SolutionIn triangle ABC, AD is perpendicular to BC. sin B = 0.8, BD = 9 cm and tan C = 1. Find the length of AB, AD, AC and DC.
View SolutionABC is a right angled triangle with ∠ABC=90∘, D is any point on AB and DE is perpendicular to AC.
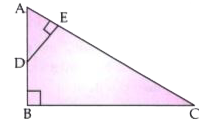
(ii) If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
View SolutionΔABC is right angled at A (Fig 11.25). AD is perpendicular to BC. If AB=5cm,BC=13 and, find the area of ΔABC Also find the lenght of AD.
View SolutionIf median of the ΔABC through A is perpendicular to BC, then which one of the following is correct ?
View SolutionIn a triangle ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB. Prove that : AD = CE.
View SolutionIn Triangle ABC, AD is perpendicular to BC, tanB=34tanC=512 and BC = 56 cm . Calculate the lengths of AD.
View SolutionABC is a right angled triangle with ABC=90∘. D is any point on AB and DE is perpendicular to AC. Prove that:

If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
View SolutionIn Δ ABC, the bisector AD of A is perpendicular to side BC (see Fig. 7.27). Show that AB = ACand ΔABCis isosceles
View Solution
