In Δ ABC, the bisector AD of A is perpendicular to side BC (see Fig. 7.27). Show that AB = ACand ΔABCis isosceles
To solve the problem, we need to show that in triangle ABC, where AD is the angle bisector of angle A and is perpendicular to side BC, the sides AB and AC are equal, thus proving that triangle ABC is isosceles.
1. Draw Triangle ABC:
- Begin by sketching triangle ABC. Label the vertices A, B, and C.
2. Draw Angle Bisector AD:
- Draw the angle bisector AD from vertex A to side BC such that AD is perpendicular to BC. Label the point where AD meets BC as D.
3. Label Angles:
- Since AD is the angle bisector, we have:
- ∠BAD=∠CAD (let's denote this angle as x).
- Also, since AD is perpendicular to BC, we have:
- ∠BDA=∠CDA=90∘.
4. Identify Triangles:
- Now, consider triangles ABD and ACD. We will show that these two triangles are congruent.
5. Use Angle-Side-Angle (ASA) Congruence:
- In triangles ABD and ACD, we have:
- AD=AD (common side),
- ∠BAD=∠CAD=x (angle bisector property),
- ∠BDA=∠CDA=90∘ (perpendicularity).
- Therefore, by the Angle-Side-Angle (ASA) criterion, triangle ABD is congruent to triangle ACD.
6. Apply Corresponding Parts of Congruent Triangles (CPCT):
- Since triangles ABD and ACD are congruent, their corresponding parts are equal. Thus, we have:
- AB=AC.
7. Conclude that Triangle ABC is Isosceles:
- Since AB=AC, triangle ABC is isosceles by definition.
Conclusion:
We have shown that AB=AC and therefore triangle ABC is isosceles.
- Begin by sketching triangle ABC. Label the vertices A, B, and C.
- Draw the angle bisector AD from vertex A to side BC such that AD is perpendicular to BC. Label the point where AD meets BC as D.
- Since AD is the angle bisector, we have:
- ∠BAD=∠CAD (let's denote this angle as x).
- Also, since AD is perpendicular to BC, we have:
- ∠BDA=∠CDA=90∘.
- Now, consider triangles ABD and ACD. We will show that these two triangles are congruent.
- In triangles ABD and ACD, we have:
- AD=AD (common side),
- ∠BAD=∠CAD=x (angle bisector property),
- ∠BDA=∠CDA=90∘ (perpendicularity).
- Therefore, by the Angle-Side-Angle (ASA) criterion, triangle ABD is congruent to triangle ACD.
- Since triangles ABD and ACD are congruent, their corresponding parts are equal. Thus, we have:
- AB=AC.
- Since AB=AC, triangle ABC is isosceles by definition.
We have shown that AB=AC and therefore triangle ABC is isosceles.
Topper's Solved these Questions
- TRIANGLESBOOK - NCERT ENGLISHCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.5
4 Videos
- TRIANGLESBOOK - NCERT ENGLISHCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.2
8 Videos
- TRIANGLESBOOK - NCERT ENGLISHCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.1
8 Videos
- SURFACE AREAS AND VOLUMESBOOK - NCERT ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - Exercise 13.9
3 Videos
Similar Questions
In ΔABC, AD is the perpendicular bisector of BC (see Fig. 7.30). Show that ΔABCis an isosceles triangle in which AB = AC.
View SolutionAD and BC are equal perpendiculars to a line segment AB (see Fig. 7.18). Show that CD bisects AB.

View SolutionIn triangle ABC,AD is perpendicular to side BC and AD2=BD×DC.
Show that angle BAC=90∘.
View SolutionIn a ΔABC, the median AD is perpendicular to AC. If b = 5 and c = 11, then a =
View SolutionABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that∠ABD =∠ACD

View SolutionIn quadrilateral ACBD, AC = ADand AB bisects ∠A(see Fig. 7.16). Show that ΔABC≅ΔABD

View SolutionD is a point on side BC of ΔABCsuch that AD = AC(see Fig. 7.47).Show that AB > AD.
View SolutionIn a triangle ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB. Prove that : AD = CE.
View SolutionABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that
(i) ΔABE≅ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.
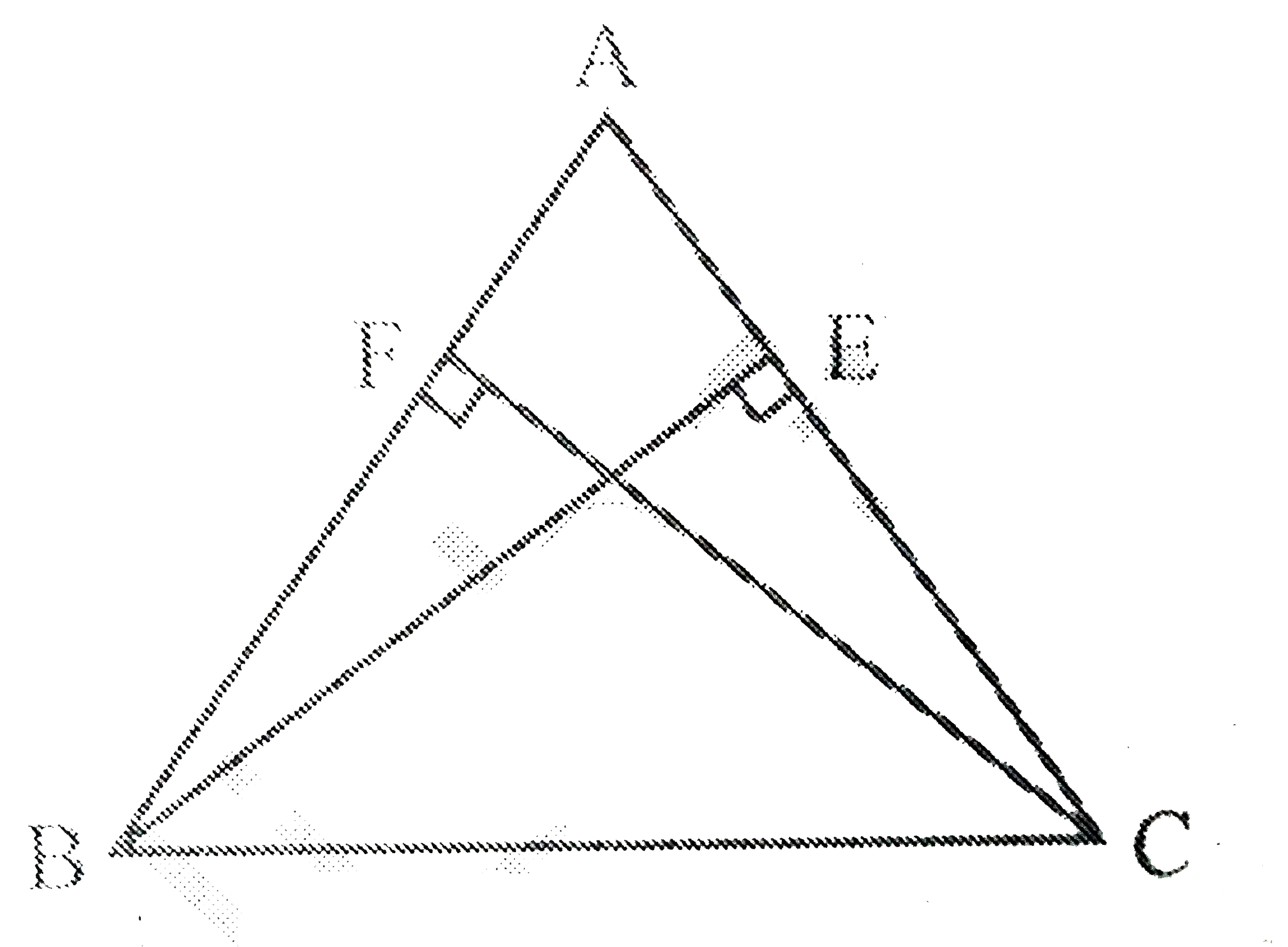
View SolutionIn an isosceles triangle ABC with AB=AC, D and E are points on BCsuch that BE=CD(see Fig. 7.29). Show that AD=AE
View Solution
