In a quadrilateral ABCD, it is being given that M is the midpoint of AC. Prove that
ar(□ABMD)=ar(□DMBC).

Median BM divides △ABC into two △ of equal area.
∴ar(△ABM)=ar(△DMC).
Median DM divides △DAC into two △ of equal area.
∴ar(△AMD)=ar(△DMC). ...(ii)
From (i) and (ii) , we get
ar(△ABM)+ar(△AMD)=ar(△BMC)+ar(△DMC)
⇒ar(□ABMD)=ar(□DMBC).
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - Exercise 11
38 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
32 Videos
- AREAS OF TRIANGLES AND QUADRILATERALSBOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
Similar Questions
Knowledge Check
In △ABC, if D is the midpoint of BC and E is the midpoint of AD then ar(△BED) = ?
 A12ar(△ABC)B13ar(△ABC)C14ar(△ABC)D23ar(△ABC)
A12ar(△ABC)B13ar(△ABC)C14ar(△ABC)D23ar(△ABC)
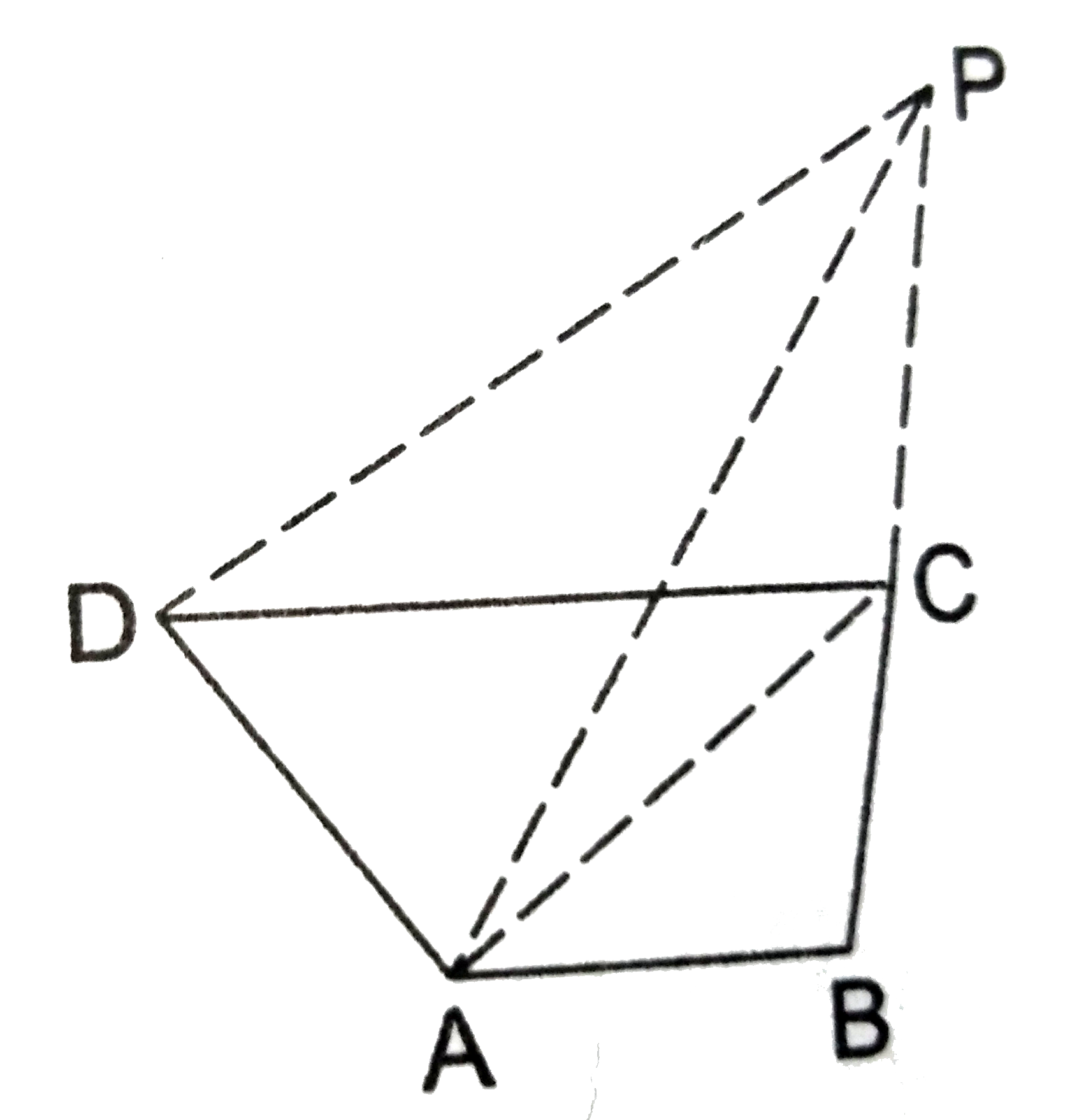
In the adjoining figure, ABCD is a quadrilateral. A line through D, parallel to AC, meets BC produced in P .
Prove that ar(△ABP)=ar(qaud. ABCD).
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way thatar(AOD)=ar(BOC).Prove that ABCD is a trapezium.
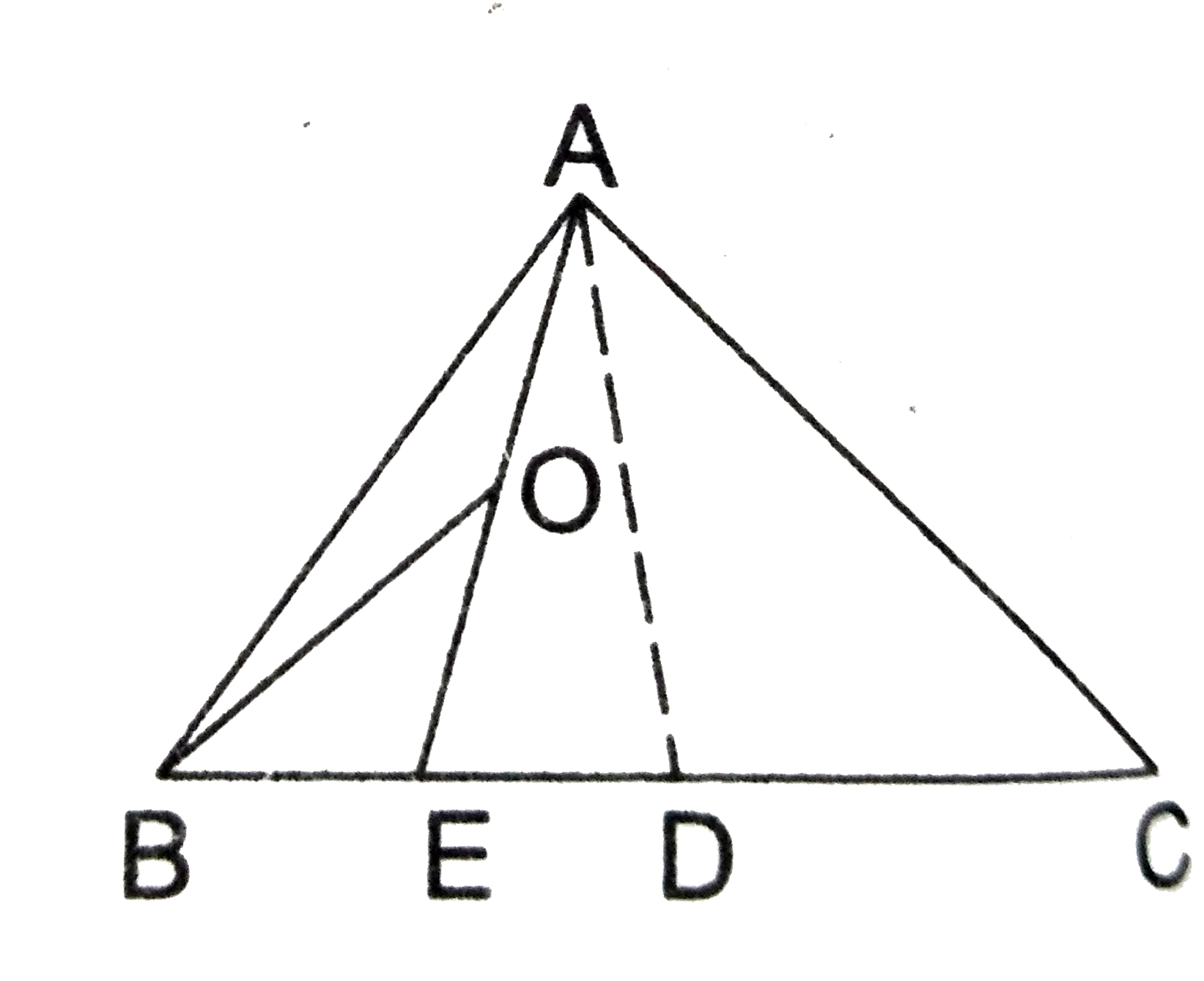
View SolutionD is the midpoint of side BC of △ABC and E is the midpoint of BD. If O is the midpoint of AE,
prove that ar(△BOE)=18ar(△ABC).
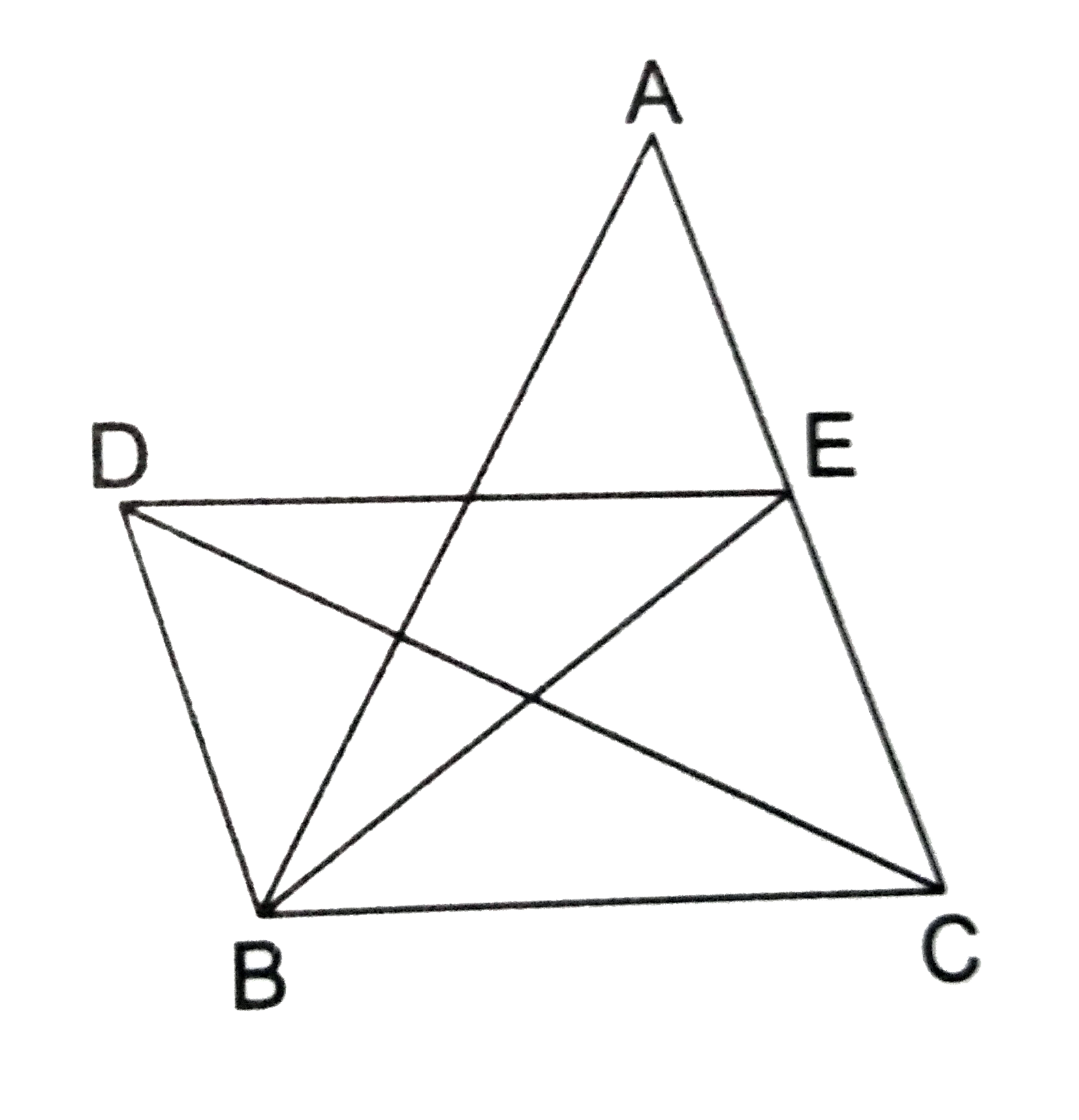
View SolutionIn the adjoining figure, BD||CA, E is the midpoint of CA and BD=12CA. Prove that
ar(△ABC)=2ar(△DBC).
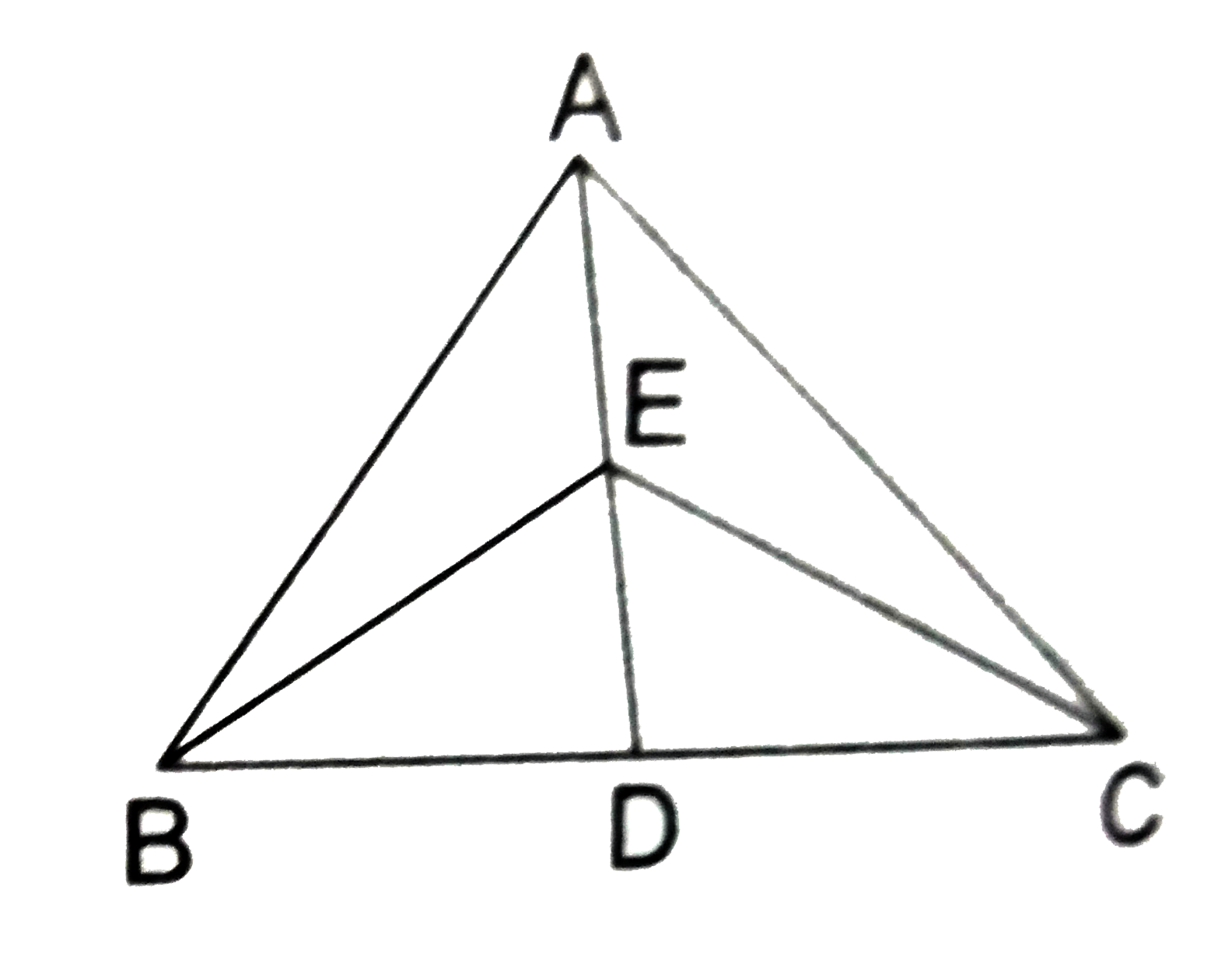
View SolutionThe vertex A of △ABC is joined to a point D on the side BC. The midpoint of AD is E.
Prove that ar(△BEC)=12ar(△ABC).
View SolutionIn Figure, APBQ CR. Prove that ar (AQC)= ar (PBR)
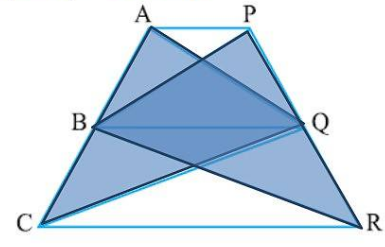
View SolutionIn the adjoining figure, ABC and BDE are two equilateral triangle such that D is the midpoint of BC. If AE intersects BC at F, show that
(i)ar(△BDE)=14ar(△ABC)
(ii)ar(△BDE)=12ar(△BAE)
(iii)ar(△ABC)=2ar(△BEC)
(iv)ar(△BFE)=ar(△AFD)
(v)ar(△BFE)=2ar(△FED)
(vi)ar(△FED)=18ar(△AFC).

View Solution


