In a quadrilateral, define each of the
following:
(i) Sides (ii) Vertices (iii) Angles
(iv) Diagonals (v) Adjacent angles
(vi) Opposite Sides (vii)Opposite sides (viii) Opposite angles (ix) Interior (x)Exterior
To define the terms related to a quadrilateral, we will consider a quadrilateral ABCD, where A, B, C, and D are the vertices of the quadrilateral. Here is a step-by-step explanation of each term:
1. Sides:
- A quadrilateral has four sides. In our quadrilateral ABCD, the sides are:
- AB (from A to B)
- BC (from B to C)
- CD (from C to D)
- DA (from D to A)
2. Vertices:
- The vertices of a quadrilateral are the points where the sides meet. For quadrilateral ABCD, the vertices are:
- A
- B
- C
- D
- Thus, there are a total of four vertices.
3. Angles:
- Angles in a quadrilateral are formed at each vertex by the intersection of two sides. For quadrilateral ABCD, the angles are:
- ∠A (angle at vertex A)
- ∠B (angle at vertex B)
- ∠C (angle at vertex C)
- ∠D (angle at vertex D)
4. Diagonals:
- Diagonals are line segments that connect non-adjacent vertices. In quadrilateral ABCD, the diagonals are:
- AC (connecting vertex A and vertex C)
- BD (connecting vertex B and vertex D)
5. Adjacent Angles:
- Adjacent angles are angles that share a common side. For quadrilateral ABCD, the adjacent angles are:
- ∠A and ∠B
- ∠B and ∠C
- ∠C and ∠D
- ∠D and ∠A
6. Opposite Sides:
- Opposite sides are sides that do not share a common vertex. In quadrilateral ABCD, the opposite sides are:
- AB and CD
- BC and DA
7. Opposite Angles:
- Opposite angles are angles that are across from each other in the quadrilateral. For quadrilateral ABCD, the opposite angles are:
- ∠A and ∠C
- ∠B and ∠D
8. Interior Angles:
- Interior angles are the angles that lie inside the quadrilateral. For quadrilateral ABCD, the interior angles are:
- ∠A, ∠B, ∠C, and ∠D
9. Exterior Angles:
- Exterior angles are the angles formed outside the quadrilateral when one side is extended. For example, if we extend side AB, the angle formed outside at vertex A is an exterior angle.
- A quadrilateral has four sides. In our quadrilateral ABCD, the sides are:
- AB (from A to B)
- BC (from B to C)
- CD (from C to D)
- DA (from D to A)
- The vertices of a quadrilateral are the points where the sides meet. For quadrilateral ABCD, the vertices are:
- A
- B
- C
- D
- Thus, there are a total of four vertices.
- Angles in a quadrilateral are formed at each vertex by the intersection of two sides. For quadrilateral ABCD, the angles are:
- ∠A (angle at vertex A)
- ∠B (angle at vertex B)
- ∠C (angle at vertex C)
- ∠D (angle at vertex D)
- Diagonals are line segments that connect non-adjacent vertices. In quadrilateral ABCD, the diagonals are:
- AC (connecting vertex A and vertex C)
- BD (connecting vertex B and vertex D)
- Adjacent angles are angles that share a common side. For quadrilateral ABCD, the adjacent angles are:
- ∠A and ∠B
- ∠B and ∠C
- ∠C and ∠D
- ∠D and ∠A
- Opposite sides are sides that do not share a common vertex. In quadrilateral ABCD, the opposite sides are:
- AB and CD
- BC and DA
- Opposite angles are angles that are across from each other in the quadrilateral. For quadrilateral ABCD, the opposite angles are:
- ∠A and ∠C
- ∠B and ∠D
- Interior angles are the angles that lie inside the quadrilateral. For quadrilateral ABCD, the interior angles are:
- ∠A, ∠B, ∠C, and ∠D
- Exterior angles are the angles formed outside the quadrilateral when one side is extended. For example, if we extend side AB, the angle formed outside at vertex A is an exterior angle.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The exterior angle of a triangle is 105∘ and one of the interior opposite angles is 60∘. Find the other two angles.
A45∘,45∘.B25∘,75∘.C45∘,55∘.D45∘,75∘.
In a triangle the greater angle has the longer side opposite to it.
View SolutionTheorem 7.2 : Angles opposite to equal sides of an isosceles triangle are equal.
View SolutionConsider the following statements: When two straight lines intersect:
(i)adjacent angles are complementary
(ii)adjacent angles are supplementary
(iii)opposite angles are equal
(iv)opposite angles are supplementary
Of those statements which is correct
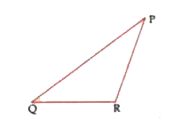
View SolutionIn the adjoining figure :
Name the angle opposite to side QR.
View SolutionIn an isosceles triangle, prove that the angles opposite to equal sides are equal.
View SolutionFind the measure of each exterior angle of a regular polygon of(i) 9 sides (ii) 15 sides
View SolutionTheorem 7.3 : The sides opposite to equal angles of a triangle are equal.
View Solution