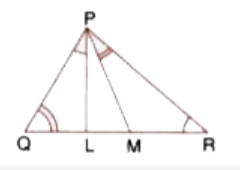
In a triangle PQR, L and M are two points on the base QR, such that ∠LPQ=∠QRP and ∠RPM=∠RQP. Prove that:
QL×RM=PL×PM
To prove that QL⋅RM=PL⋅PM in triangle PQR with points L and M on base QR, where ∠LPQ=∠QRP and ∠RPM=∠RQP, we can follow these steps:
Step 1: Identify the triangles
We have triangle PQR with points L and M on QR. We know that:
- ∠LPQ=∠QRP (Given)
- ∠RPM=∠RQP (Given)
Step 2: Establish similarity of triangles
From the given angles, we can establish that:
- Triangle PQL and triangle RPM are similar by the Angle-Angle (AA) criterion of similarity.
Step 3: Write the proportion of sides
Since the triangles PQL and RPM are similar, the corresponding sides are in proportion. Therefore, we can write:
PQRP=QLPM=PLRM
Step 4: Cross-multiply the proportions
From the proportion established, we can cross-multiply:
QL⋅RP=PL⋅PM
Also, we can express RP in terms of QR:
QR=QL+RM
However, for our proof, we will focus on the relationship derived from the similarity.
Step 5: Rearranging the equation
From the cross-multiplication, we can rearrange it to show:
QL⋅RM=PL⋅PM
Conclusion
Thus, we have proved that:
QL⋅RM=PL⋅PM
We have triangle PQR with points L and M on QR. We know that:
- ∠LPQ=∠QRP (Given)
- ∠RPM=∠RQP (Given)
From the given angles, we can establish that:
- Triangle PQL and triangle RPM are similar by the Angle-Angle (AA) criterion of similarity.
Since the triangles PQL and RPM are similar, the corresponding sides are in proportion. Therefore, we can write:
PQRP=QLPM=PLRM
From the proportion established, we can cross-multiply:
QL⋅RP=PL⋅PM
Also, we can express RP in terms of QR:
QR=QL+RM
However, for our proof, we will focus on the relationship derived from the similarity.
From the cross-multiplication, we can rearrange it to show:
QL⋅RM=PL⋅PM
Thus, we have proved that:
QL⋅RM=PL⋅PM
Topper's Solved these Questions
- MIXED PRACTICE BOOK - ICSECHAPTER - MIXED PRACTICE EXERCISE - SET B
52 Videos
- MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)BOOK - ICSECHAPTER - MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)EXERCISE - EXERCISE 24 (E)
23 Videos
- PROBABILITYBOOK - ICSECHAPTER - PROBABILITYEXERCISE - EXERCISE 25(C)
106 Videos
Similar Questions
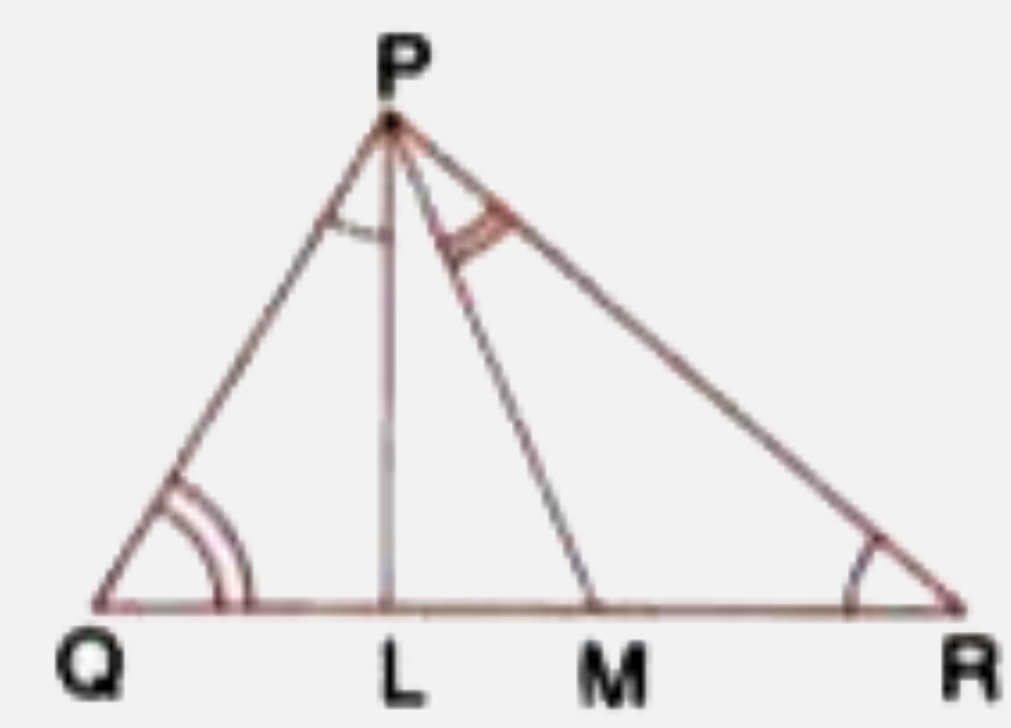
In a triangle PQR, L and M are two points on the base QR, such that ∠LPQ=∠QRP and ∠RPM=∠RQP. Prove that:
PQ2=QR×QL
View SolutionIn a triangle PQR, L and M are two points on the base QR, such that ∠LPQ=∠QRP and ∠RPM=∠RQP. Prove that:
ΔPQL~ΔRPM
View SolutionIn a triangle PQR, L and M are two points on the base QR, such that ∠LPQ=∠QRP and ∠RPM=∠RQP. Prove that:

QL×RM=PL×PM
View SolutionIn a triangle PQR, L and M are two points on the base QR, such that ∠LPQ=∠QRP and ∠RPM=∠RQP. Prove that:
PQ2=QR×QL
View SolutionIn a triangle PQR, L and M are two points on the base QR, such that ∠LPQ=∠QRP and ∠RPM=∠RQP. Prove that:
ΔPQL~ΔRPM
View SolutionThe sides PQ, PR of triangle PQR are equal, and S, T are points on PR, PQ such that ∠PSQand∠PTR are right angles
If OS and RT intersect at M, prove that the triangles PTM and PSM are congruent.
View SolutionIn triangle PQR, if PQ=RQ and L, M and N are the mid-points of the sides PQ, QR and RP respectively. Prove that LN=MN.
View SolutionIn a △ ABC, If L and M are points on AB and AC respectively such that LM∣∣BC. Prove that: ar (△ LOB)=ar (△ MOC)
View SolutionIn triangle ABC, the medians BP and CQ are produced upto points M and N respectively such that BP = PM and CQ = QN. Prove that:
M, A and N are collinear.
View SolutionIn ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.
View Solution
