In a triangle PQR, L and M are two points on the base QR, such that ∠LPQ=∠QRP and ∠RPM=∠RQP. Prove that:
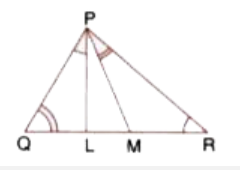
PQ2=QR×QL
Step by step video & image solution for In a triangle PQR, L and M are two points on the base QR, such that /_LPQ = /_QRP and /_RPM = /_RQP. Prove that: PQ^2 = QR xx QL by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(D)
18 Videos
- SIMILARITY BOOK - ICSECHAPTER - SIMILARITY EXERCISE - MULTIPLE CHOICE QUESTIONS (COMPETENCY BASED QUESTIONS)
10 Videos
- SOLVING (SIMPLE) PROBLEMS (BASED ON QUADRATIC EQUATIONS)BOOK - ICSECHAPTER - SOLVING (SIMPLE) PROBLEMS (BASED ON QUADRATIC EQUATIONS)EXERCISE - Exercise 6(e )
18 Videos
Similar Questions
In a triangle PQR, L and M are two points on the base QR, such that ∠LPQ=∠QRP and ∠RPM=∠RQP. Prove that:

QL×RM=PL×PM
View SolutionIn a triangle PQR, L and M are two points on the base QR, such that ∠LPQ=∠QRP and ∠RPM=∠RQP. Prove that:
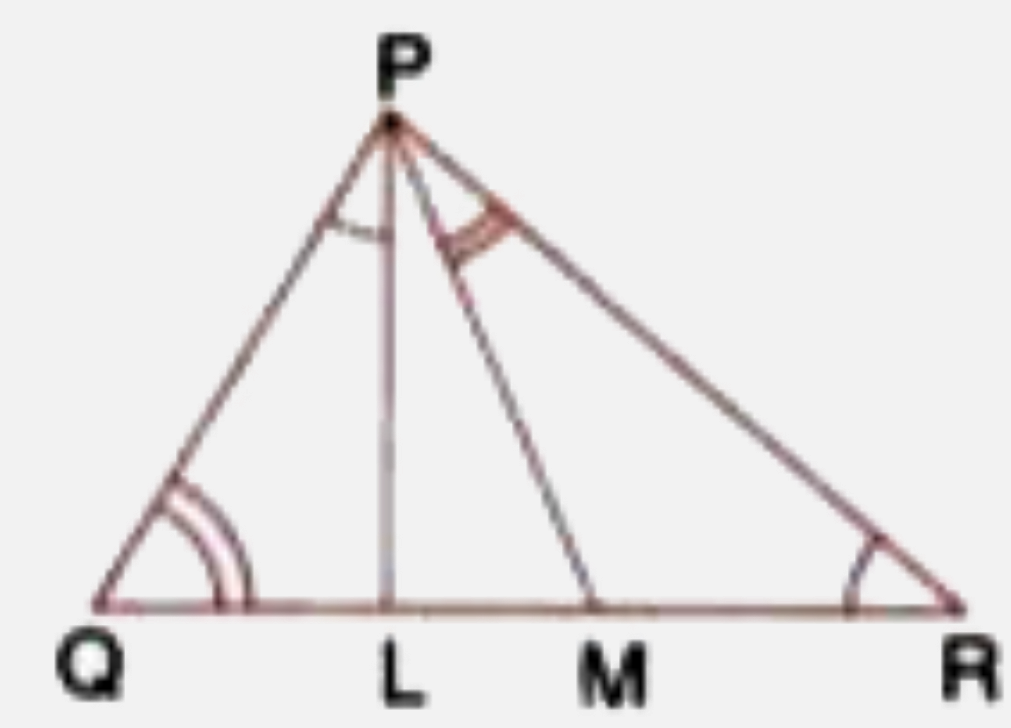
ΔPQL~ΔRPM
View SolutionIn a triangle PQR, L and M are two points on the base QR, such that ∠LPQ=∠QRP and ∠RPM=∠RQP. Prove that:
PQ2=QR×QL
View SolutionIn a triangle PQR, L and M are two points on the base QR, such that ∠LPQ=∠QRP and ∠RPM=∠RQP. Prove that:
QL×RM=PL×PM
View SolutionIn a triangle PQR, L and M are two points on the base QR, such that ∠LPQ=∠QRP and ∠RPM=∠RQP. Prove that:
ΔPQL~ΔRPM
View SolutionABCD is a square. P, Q and Rare the points on AB, BC and CD respectively, such that AP = BQ = CR. Prove that:
PQ = QR
View SolutionPQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR=∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.

Prove ΔPQR~ΔSPR.
View SolutionS and T are points on sides PR and QR of ΔPQR such that ∠P=∠RTS Show that ΔRPQ~ΔRTS
View SolutionIn quadrilateral PQRS , PS = QR and ∠SPQ=∠RQP . Prove that :
PR=QS
View SolutionPQR is a triangle right-angled at P and M is a point on QR such that PM⊥QR. Show thatPM2=QM.MR.
View Solution