In an equilateral △ABC,AD is the altitude drawn from A on the side BC. Prove that 3AB2=4AD2
Step by step video & image solution for In an equilateral triangleABC, AD is the altitude drawn from A on the side BC. Prove that 3AB^(2) = 4AD^(2) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Revision Exercise very shot Questions
1 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Revision Exercise Very Short Questions
9 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Exercise 6c
10 Videos
- STATISTICS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
4 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
In ΔABC,'h' is the length of altitude drawn from vertex A on the side BC. Prove that:
2(b2+c2)≥4h2+a2. Also, discuss the case when equality holds true.
View SolutionIn an equilateral triangle ABC, BE is perpendicular to side CA. Prove that:
AB2+BC2+CA2=4BE2
View SolutionIn a △ABC,B=π8,C=5π8. The altitude from A to the side BC, is
View SolutionIn a scalene triangle ABC , AD and CF are the altitudes drawn from A and C on the sides BC and AB repectively.If the area of the triangle ABC and BDF are 18sq.units and 2 sq. units respectively and DF = 2√2 , then R =
View SolutionIn acute angled triangle ABC, AD is median and AE is altitude , prove that:
(i) AC2=AD2+BC×DE+14BC2
(ii) AB2=AD2−BC×DE+14BC2
(iii) AC2+AB2=2AD2+12BC2
View SolutionIn an acute angled triangle ABC, AD is the median in it. then :
AD2 =
View SolutionAD is an altitude of an equilateral triangle ABC. On AD as base, another equilateral triangle ADE is constructed. Prove that Area ( triangle ADE ): Area ( triangle ABC )=3:4.
View SolutionThe following figure shows a triangle ABC in which AD is a median and AE⊥BC. Prove that 2AB2+2AC2=4AD2+BC2 .
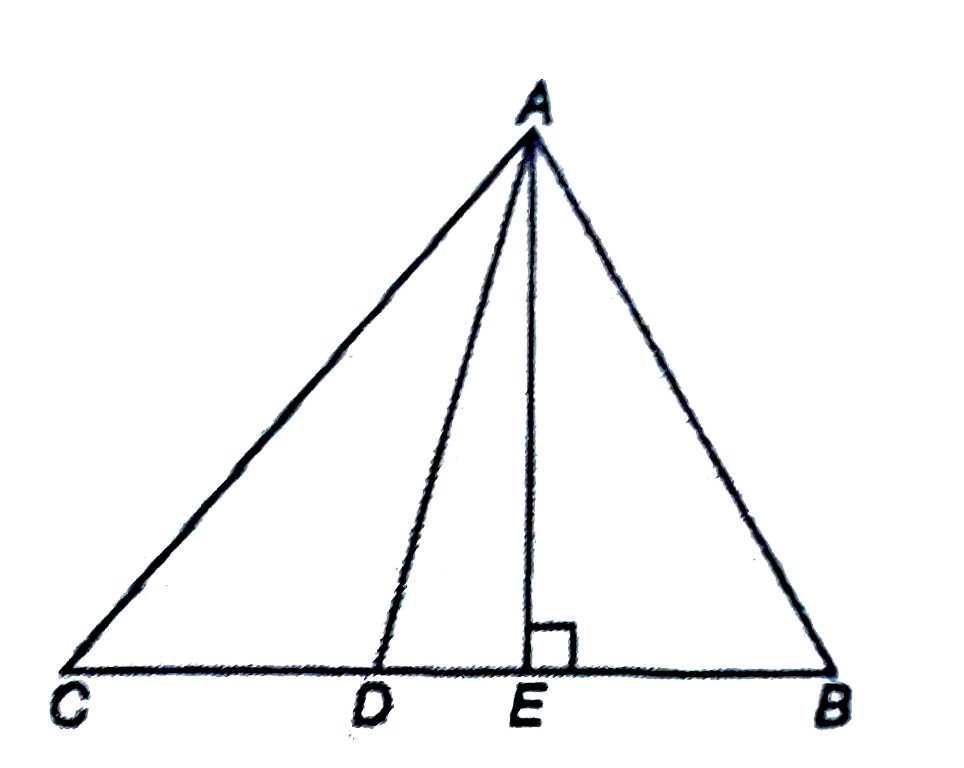
View SolutionIn an equilateral triangle with side a, prove that the altitude is of length a√32
View SolutionIn a right triangle ABC, right angled at A, AD is drawn perpendicular to BC. Prove that:
AB2−BD2=AC2−CD2
View Solution
