In ΔABC, the perependicular from A BC meets BC at D such that BD=7cmandDC=12cm.Find the ratio of the areas of the triangles ABD and ADC.
The correct Answer is:38 cm
Step by step video, text & image solution for In Delta ABC, the perependicular from A BC meets BC at D such that BD =7 cm and DC = 12 cm. Find the ratio of the areas of the triangles ABD and ADC. by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - PERIMETER AND AREA EXERCISE - EXERCISE 17.316videos
PERIMETER AND AREA
- BOOK - ICSECHAPTER - PERIMETER AND AREA EXERCISE - REVISION EXERCISE24videos
PERIMETER AND AREA
- BOOK - ICSECHAPTER - PERIMETER AND AREA EXERCISE - EXERCISE 17.115videos
PERIMETER AND AREA
- BOOK - ICSECHAPTER - PERCENTAGE, PROFIT AND LOSSEXERCISE - REVISION EXERCISE26videos
PERCENTAGE, PROFIT AND LOSS
- BOOK - ICSECHAPTER - PROBABILITYEXERCISE - TRY THIS14videos
PROBABILITY
Similar Questions
A triangle ABC is such that AD is perpendicular to BC and E is a point on DC. Also. Given that BD=2cm,DE=4cm,andEC=8cm. Find the ratio of the areas of ΔABC , ΔADEandΔAEC.
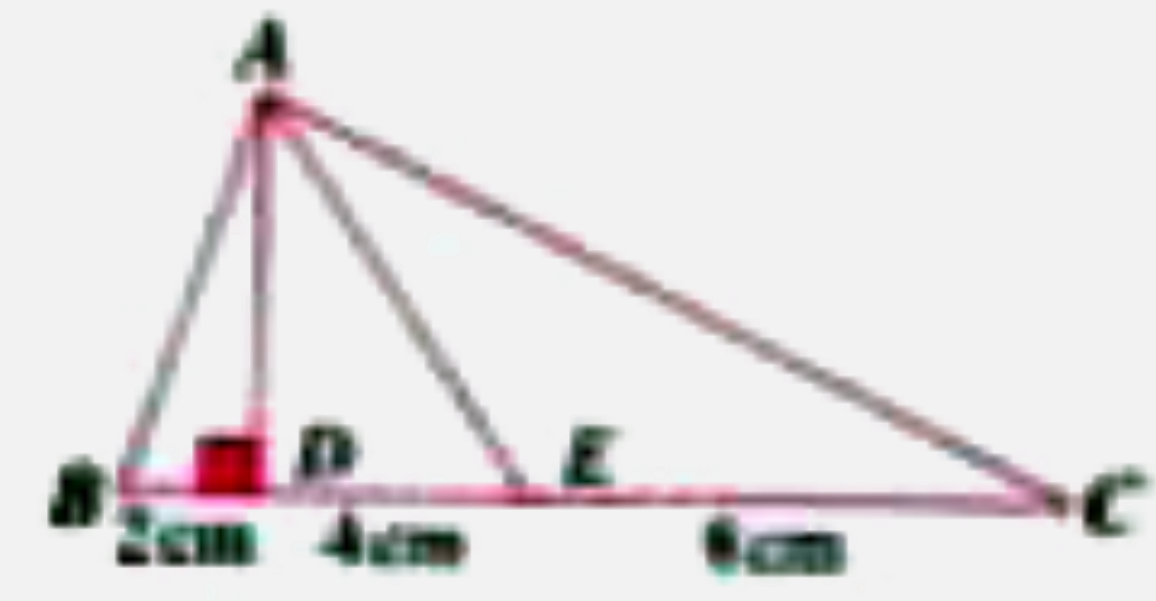 View Solution
View SolutionIn triangle ABC, AD is perpendicular to BC. sin B = 0.8, BD = 9 cm and tan C = 1. Find the length of AB, AD, AC and DC.
View Solution
Knowledge Check
- Question 1 - Select One
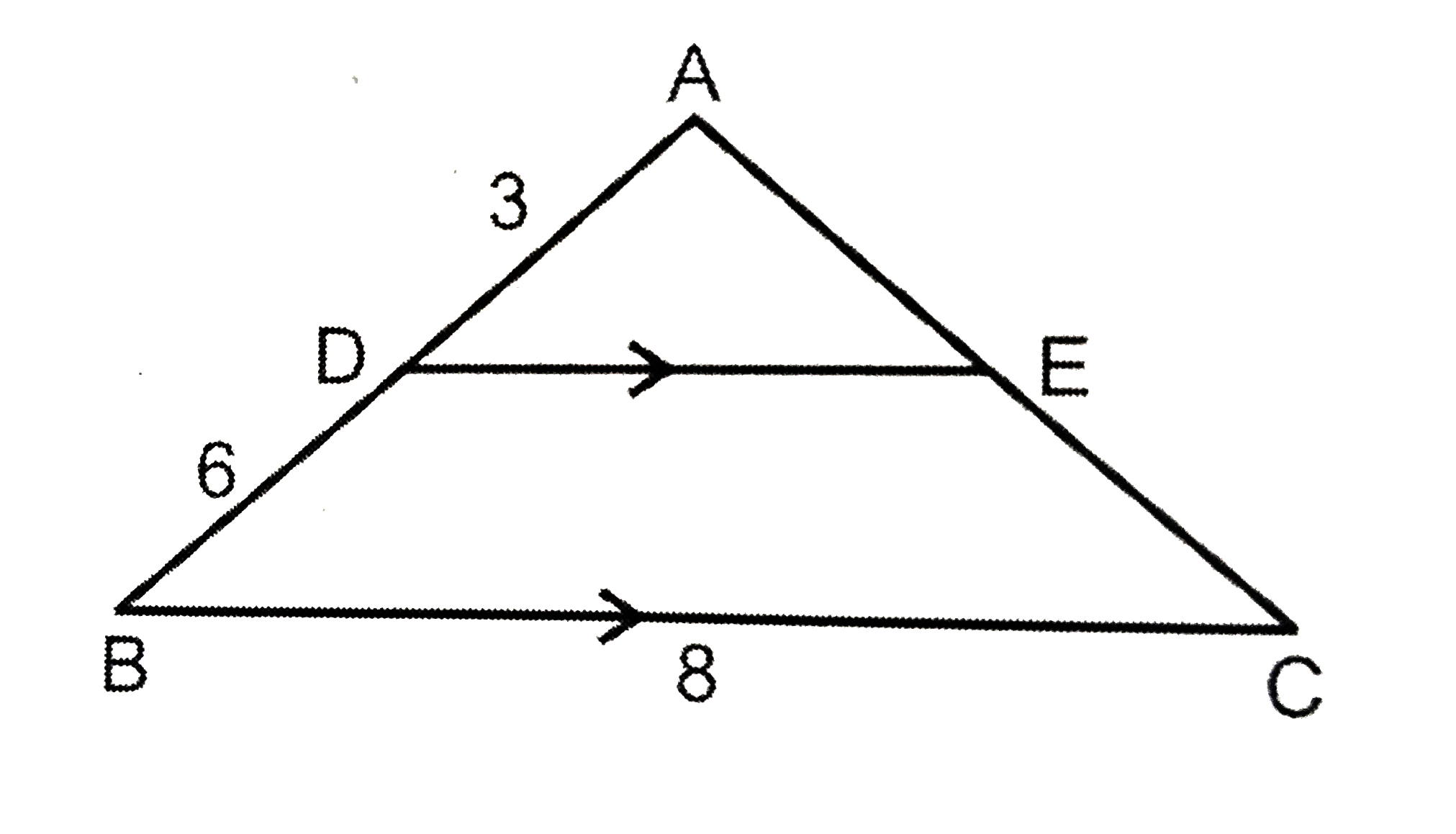
In the ΔABC,DE||BC, AD=3, BD=6, and BC=8. What is the ratio of the areas of triangle ADE and trapezium BDEC?A1:3B1:4C1:8D1:9
ΔABC is right-angled at C. If AC=5cmandBC=12cm find the length of AB.
View SolutionConstruct Δ ABC with AB = 4.5 cm, BC = 7 cm and CA = 6 cm.
View SolutionIn triangle ABC, AB = AC = 15 cm and BC = 18 cm. Find :
cos BView SolutionIn triangle ABC,AD is perpendicular to side BC and AD2=BD×DC.
Show that angle BAC=90∘.View SolutionIn a triangle ABC , AP is perpendicular to BC . If BC = 112 cm , cot B =43 and cot C =125 , calculate the length of AP
View SolutionIn ΔABC,AD and CE are perpendiculars from A and C on the opposite sides. If AD=6cm.BC=14cm,AB=10cm,find CE.
View SolutionIn triangle ABC, AB = AC = 15 cm and BC = 18 cm. Find :
sin CView Solution

