In a triangle ABC , AP is perpendicular to BC . If BC = 112 cm , cot B =43 and cot C =125 , calculate the length of AP
The correct Answer is:AP = 30 cm
To find the length of AP in triangle ABC, we will follow these steps:
Step 1: Understand the given information
We have a triangle ABC where AP is perpendicular to BC. We know:
- BC = 112 cm
- cot B = 4/3
- cot C = 12/5
Step 2: Relate cotangent to the sides
From trigonometry, we know that:
- cot B = BP / AP
- cot C = CP / AP
Step 3: Express BP and CP in terms of AP
Using the given values of cot B and cot C:
1. From cot B = 4/3, we can write:
BP=43AP
2. From cot C = 12/5, we can write:
CP=125AP
Step 4: Set up an equation for BC
Since BP + CP = BC, we can substitute the expressions we found:
BP+CP=43AP+125AP=112
Step 5: Find a common denominator and combine the fractions
The least common multiple of 3 and 5 is 15. We will convert both fractions:
43AP=2015AP
125AP=3615AP
Now we can add them:
2015AP+3615AP=5615AP
So we have:
5615AP=112
Step 6: Solve for AP
To isolate AP, we multiply both sides by 15:
56AP=112×15
Now, divide both sides by 56:
AP=112×1556
Step 7: Simplify the expression
Calculating the right side:
AP=168056=30
Conclusion
The length of AP is 30 cm.
---
We have a triangle ABC where AP is perpendicular to BC. We know:
- BC = 112 cm
- cot B = 4/3
- cot C = 12/5
From trigonometry, we know that:
- cot B = BP / AP
- cot C = CP / AP
Using the given values of cot B and cot C:
1. From cot B = 4/3, we can write:
BP=43AP
2. From cot C = 12/5, we can write:
CP=125AP
Since BP + CP = BC, we can substitute the expressions we found:
BP+CP=43AP+125AP=112
The least common multiple of 3 and 5 is 15. We will convert both fractions:
43AP=2015AP
125AP=3615AP
Now we can add them:
2015AP+3615AP=5615AP
So we have:
5615AP=112
To isolate AP, we multiply both sides by 15:
56AP=112×15
Now, divide both sides by 56:
AP=112×1556
Calculating the right side:
AP=168056=30
The length of AP is 30 cm.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - TRIGONOMETRICAL RATIOS EXERCISE - EXERCISE 22(A)47videos
TRIGONOMETRICAL RATIOS
- BOOK - ICSECHAPTER - TRIGONOMETRICAL RATIOS EXERCISE - EXERCISE 22(B)50videos
TRIGONOMETRICAL RATIOS
- BOOK - ICSECHAPTER - TRIANGLES EXERCISE - 4 MARKS QUESTIONS24videos
TRIANGLES
- BOOK - ICSECHAPTER - TRIGONOMETRICAL RATIOS OF STANDARD ANGLESEXERCISE - EXERCISE 23(C)118videos
TRIGONOMETRICAL RATIOS OF STANDARD ANGLES
Similar Questions
In Triangle ABC, AD is perpendicular to BC, tanB=34tanC=512 and BC = 56 cm . Calculate the lengths of AD.
View SolutionIn triangle ABC, given below, AB = 8 cm, BC = 6 cm and AC = 3 cm. Calculate the length of OC
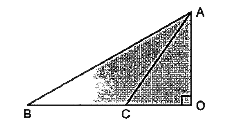 View Solution
View SolutionIn a triangle ABC , if 3a = b + c , then cot B2 cot C2 =
View SolutionIn the given figure, BC is parallel to DE. Area of triangle ABC=25cm2, Area of trapezium BCED=24cm2andDE=14cm. Calculate the length of BC.
Also, find the area of triangle BCD.
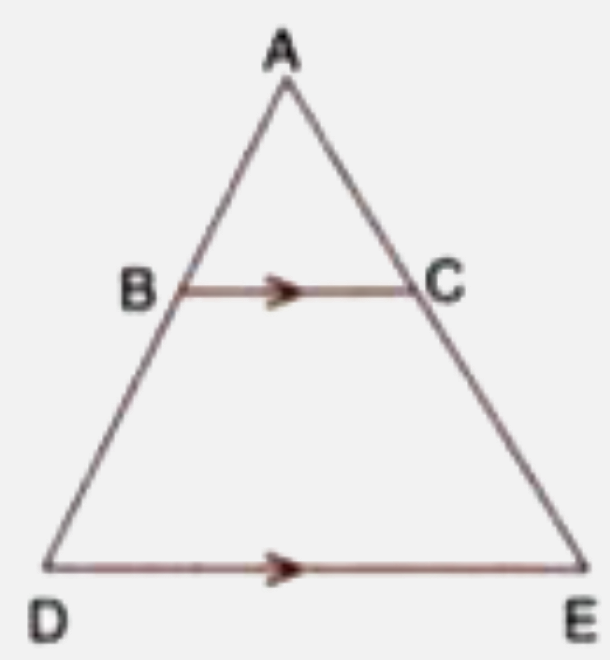 View Solution
View SolutionAP, AQ and BC are tangents to the circle. If AB = 5 cm, AC = 6 cm and BC = 4 cm, then the length of AP (in cm) is
View SolutionAP, AQ and BC are tangents to the circle. If AB = 5 cm, AC = 6 cm and BC = 4 cm, then the length of AP (in cm) is
View SolutionThe given diagram shows two isosceles triangles which are similar. In the given diagram, PQ and BC are not parallel, PC = 4, AQ = 3, QB = 12, BC = 15 and AP = PQ. Calculate :
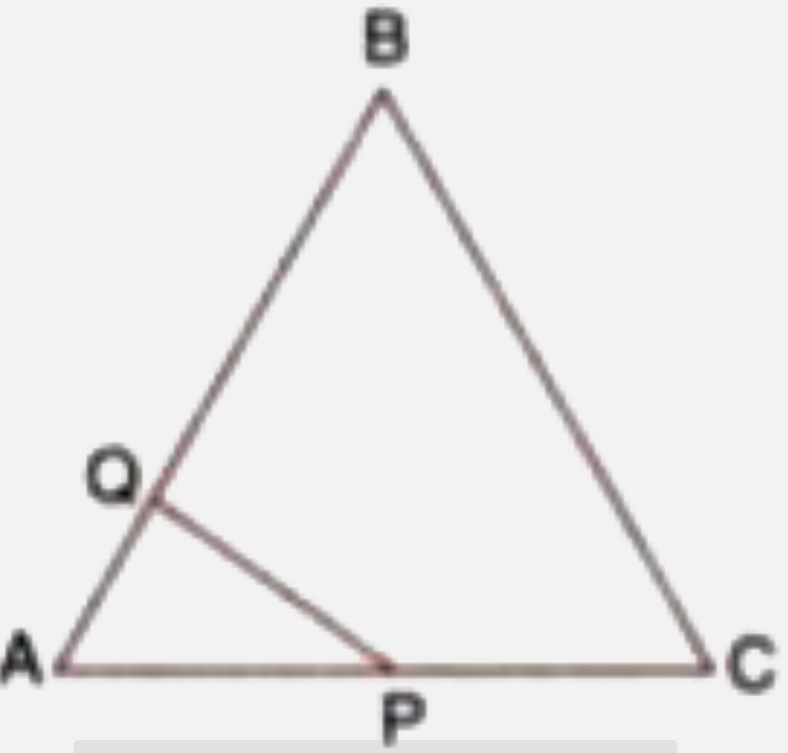
the length of AP.View SolutionΔABC is right-angled at C. If AC=5cmandBC=12cm find the length of AB.
View SolutionConstruct a triangle ABC given that :
BC = 4 . 5 cm, AB = 5 . 2 cm and CA = 3 . 8 cmView SolutionIn ΔABC, the perependicular from A BC meets BC at D such that BD=7cmandDC=12cm.Find the ratio of the areas of the triangles ABD and ADC.
View Solution

