In triangle ABC,AD is perpendicular to side BC and AD2=BD×DC.
Show that angle BAC=90∘.
To solve the problem, we need to show that in triangle ABC, if AD is perpendicular to side BC and AD2=BD×DC, then angle BAC=90∘.
1. Understanding the Given Information:
- We have triangle ABC.
- AD is perpendicular to BC, meaning ∠ADB=90∘.
- We are given that AD2=BD×DC.
2. Applying the Pythagorean Theorem:
- In right triangle ADB:
AB2=AD2+BD2(1)
- In right triangle ADC:
AC2=AD2+DC2(2)
3. Substituting AD2:
- From the given condition AD2=BD×DC, we can substitute AD2 in equations (1) and (2):
- From equation (1):
AB2=BD×DC+BD2(3)
- From equation (2):
AC2=BD×DC+DC2(4)
4. Adding Equations (3) and (4):
- Now, we add equations (3) and (4):
AB2+AC2=(BD×DC+BD2)+(BD×DC+DC2)
- Simplifying this gives:
AB2+AC2=2(BD×DC)+BD2+DC2
5. Using the Identity:
- Notice that BD2+DC2=(BD+DC)2−2(BD×DC). Thus, we can rewrite the equation:
AB2+AC2=2(BD×DC)+(BD+DC)2−2(BD×DC)
- This simplifies to:
AB2+AC2=(BD+DC)2
6. Identifying BC:
- Since BC=BD+DC, we have:
AB2+AC2=BC2
7. Conclusion:
- By the Pythagorean theorem, since AB2+AC2=BC2, triangle ABC is a right triangle with the right angle at A.
- Therefore, we conclude that:
∠BAC=90∘
- We have triangle ABC.
- AD is perpendicular to BC, meaning ∠ADB=90∘.
- We are given that AD2=BD×DC.
- In right triangle ADB:
AB2=AD2+BD2(1)
- In right triangle ADC:
AC2=AD2+DC2(2)
- From the given condition AD2=BD×DC, we can substitute AD2 in equations (1) and (2):
- From equation (1):
AB2=BD×DC+BD2(3)
- From equation (2):
AC2=BD×DC+DC2(4)
- Now, we add equations (3) and (4):
AB2+AC2=(BD×DC+BD2)+(BD×DC+DC2)
- Simplifying this gives:
AB2+AC2=2(BD×DC)+BD2+DC2
- Notice that BD2+DC2=(BD+DC)2−2(BD×DC). Thus, we can rewrite the equation:
AB2+AC2=2(BD×DC)+(BD+DC)2−2(BD×DC)
- This simplifies to:
AB2+AC2=(BD+DC)2
- Since BC=BD+DC, we have:
AB2+AC2=BC2
- By the Pythagorean theorem, since AB2+AC2=BC2, triangle ABC is a right triangle with the right angle at A.
- Therefore, we conclude that:
∠BAC=90∘
Topper's Solved these Questions
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(B)
17 Videos
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(C)
24 Videos
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(E)
61 Videos
- SIMILARITY BOOK - ICSECHAPTER - SIMILARITY EXERCISE - MULTIPLE CHOICE QUESTIONS (COMPETENCY BASED QUESTIONS)
10 Videos
- SOLVING (SIMPLE) PROBLEMS (BASED ON QUADRATIC EQUATIONS)BOOK - ICSECHAPTER - SOLVING (SIMPLE) PROBLEMS (BASED ON QUADRATIC EQUATIONS)EXERCISE - Exercise 6(e )
18 Videos
Similar Questions
In triangles ABC , AD is perpendicular to BC and AD2=BD×DC . Prove that angle BAC=90∘
View SolutionIn triangle ABC, AD is perpendicular to BC. sin B = 0.8, BD = 9 cm and tan C = 1. Find the length of AB, AD, AC and DC.
View SolutionIn Triangle ABC, AD is perpendicular to BC, tanB=34tanC=512 and BC = 56 cm . Calculate the lengths of AD.
View SolutionIn ΔABC,AB=ACandD is a point an side AC such that AD = BD = BC . Show that : ∠ADB=108∘
View SolutionIn a triangle ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB. Prove that : AD = CE.
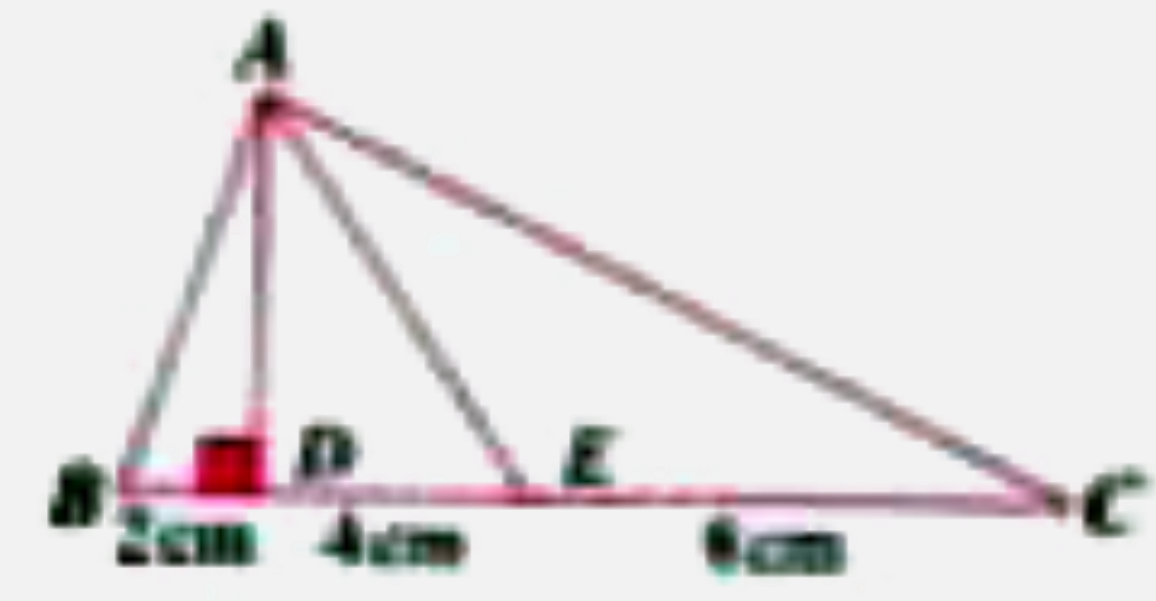
View SolutionA triangle ABC is such that AD is perpendicular to BC and E is a point on DC. Also. Given that BD=2cm,DE=4cm,andEC=8cm. Find the ratio of the areas of ΔABC , ΔADEandΔAEC.
View SolutionThe following figure shows a triangle ABC in which AD and BE are perpendiculars to BC and AC respectively. Show that :
CA×CE=CB×CD

View SolutionThe following figure shows a triangle ABC in which AD and BE are perpendiculars to BC and AC respectively. Show that :
ΔADC~ΔBEC

View SolutionIn Δ ABC, the bisector AD of A is perpendicular to side BC (see Fig. 7.27). Show that AB = ACand ΔABCis isosceles
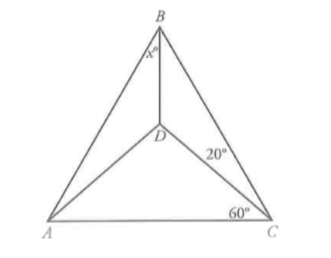
View SolutionIn triangle ABC,AD=BD=CD (See figure). What is x?
View Solution
