In ΔPQR,PR=8cm,QR=4cmandPL=5cm (Fig 11.22). Find: (i) the area of the ΔPQR (ii) QM
To solve the problem step by step, we will find the area of triangle PQR and then calculate the length of QM.
Step 1: Calculate the Area of Triangle PQR
1. Identify the base and height:
- The base of triangle PQR is QR, which measures 4 cm.
- The height corresponding to this base is PL, which measures 5 cm.
2. Use the area formula for a triangle:
- The formula for the area of a triangle is given by:
Area=12×base×height
3. Substitute the values into the formula:
- Here, base = QR = 4 cm and height = PL = 5 cm.
- Thus, the area can be calculated as:
Area=12×4×5
4. Calculate the area:
- First, calculate 12×4=2.
- Then, multiply by 5:
2×5=10 cm2
Step 2: Find the Length of QM
1. Understand the relationship between area and height:
- We know that the area of triangle PQR can also be expressed using the base PR and height QM.
- The formula for the area using base PR is:
Area=12×base×height
- Here, base = PR = 8 cm and height = QM (which we need to find).
2. Set up the equation:
- We already calculated the area of triangle PQR as 10 cm². Therefore, we can set up the equation:
10=12×8×QM
3. Solve for QM:
- First, simplify the equation:
10=4×QM
- Now, divide both sides by 4:
QM=104=2.5 cm
Final Answers:
(i) The area of triangle PQR is 10 cm2.
(ii) The length of QM is 2.5 cm.
- The base of triangle PQR is QR, which measures 4 cm.
- The height corresponding to this base is PL, which measures 5 cm.
- The formula for the area of a triangle is given by:
Area=12×base×height
- Here, base = QR = 4 cm and height = PL = 5 cm.
- Thus, the area can be calculated as:
Area=12×4×5
- First, calculate 12×4=2.
- Then, multiply by 5:
2×5=10 cm2
- We know that the area of triangle PQR can also be expressed using the base PR and height QM.
- The formula for the area using base PR is:
Area=12×base×height
- Here, base = PR = 8 cm and height = QM (which we need to find).
- We already calculated the area of triangle PQR as 10 cm². Therefore, we can set up the equation:
10=12×8×QM
- First, simplify the equation:
10=4×QM
- Now, divide both sides by 4:
QM=104=2.5 cm
(i) The area of triangle PQR is 10 cm2.
(ii) The length of QM is 2.5 cm.
Topper's Solved these Questions
- PERIMETER AND AREABOOK - NCERT ENGLISHCHAPTER - PERIMETER AND AREAEXERCISE - EXERCISE 11.1
8 Videos
- PERIMETER AND AREABOOK - NCERT ENGLISHCHAPTER - PERIMETER AND AREAEXERCISE - EXERCISE 11.4
8 Videos
- LINES AND ANGLESBOOK - NCERT ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - EXERCISE 5.2
6 Videos
- RATIONAL NUMBERSBOOK - NCERT ENGLISHCHAPTER - RATIONAL NUMBERSEXERCISE - EXERCISE 9.2
4 Videos
Similar Questions
Knowledge Check
In ΔPQR,PQ=x,QR=x+3, and PR=y. If x=y+3, then which one of the following is true?
A∠P<∠Q<∠RB∠Q<∠R<∠PC∠R<∠P<∠QD∠P<∠R<∠Q
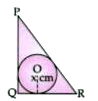
In triangle PQR, PQ = 24 cm, QR = 7 cm and ∠PQR=90∘. Find the radius of the inscribed circle.
View SolutionThe perpendicular from P and QR in the triangle jPQR meets QR at S. Alsl, T is a point on SR sch that QS =3cm,ST=4cm,andT=8cm. Find the ratio of the areas of the triangles PQS , PST and PTR.
View SolutionA circle is inscribed in a triangle PQR with PQ = 10 cm, QR = 8 cm and PR = 12 cm. Find the lengths QM, RN and PL.
View SolutionA circle is inscribed in a triangle PQR with PQ = 10 cm, QR = 8 cm and PR = 12 cm. Find the lengths QM, RN and PL.
View SolutionPQRS is a parallelogram (Fig11.23).QM is the height from Q to SRandQN is the height from Q to PS. If SR=12cmandQM=8cm. Find : (a)theareaoftheparal≤gramPQRS(b)QN,ifPS=8cm
View SolutionPQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR=∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.

area of ΔPQRarea of ΔSPR
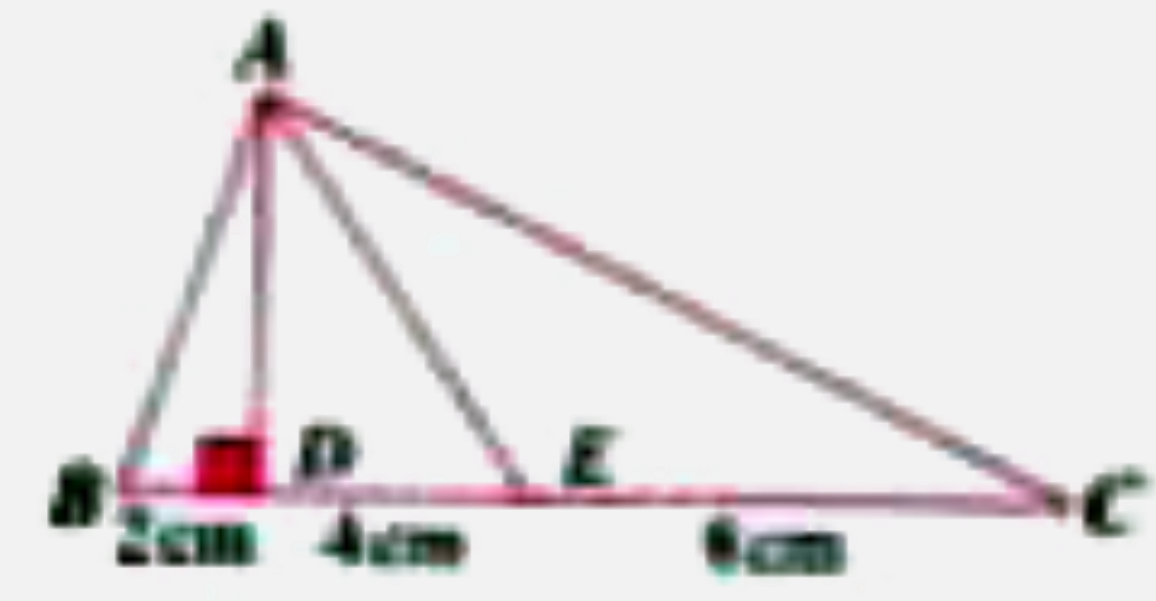
View SolutionA triangle ABC is such that AD is perpendicular to BC and E is a point on DC. Also. Given that BD=2cm,DE=4cm,andEC=8cm. Find the ratio of the areas of ΔABC , ΔADEandΔAEC.
View Solution
